Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
Specialization of Cremona transformations
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 171-177
- Print publication:
- December 1968
-
- Article
- Export citation
On Hausdorff dimension of projections
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-155
- Print publication:
- December 1968
-
- Article
- Export citation
Irrotational gravity waves of finite height: a numerical study
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 139-148
- Print publication:
- December 1968
-
- Article
- Export citation
Linear forms in the logarithms of algebraic numbers (IV)
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 204-216
- Print publication:
- December 1968
-
- Article
- Export citation
Corrigendum: Mathematika Volume 14, 1967
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, p. 227
- Print publication:
- December 1968
-
- Article
-
- You have access
- Export citation
MTK volume 15 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1968
-
- Article
-
- You have access
- Export citation
On nodes of degree two in random trees
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 188-192
- Print publication:
- December 1968
-
- Article
- Export citation
Integral domains in which each non-zero ideal is divisorial
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 164-170
- Print publication:
- December 1968
-
- Article
- Export citation
The limiting behavior of transient birth and death processes conditioned on survival
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 716-722
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
On rings of sets
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 723-730
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
Maximal connected topologies
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 700-705
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
The serial correlation coefficients of waiting times in a stationary single server queue
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 683-699
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
On a many server queue with non-recurrent input and negative exponential servers
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 706-715
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
On asymptotic properties of sub-critical branching processes
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 671-682
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
0-dimensional compactifications and Boolean rings
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 755-765
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
Contents
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 766-768
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
Distinguished submodules
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 661-670
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
A note on commutative semigroups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 731-736
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
JAZ volume 8 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
JAZ volume 8 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
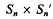 of two
of two 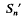 (regarded as an irreducible algebraic system of ∞
(regarded as an irreducible algebraic system of ∞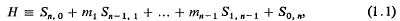
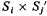 of
of 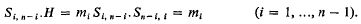
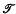
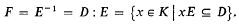
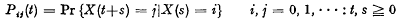
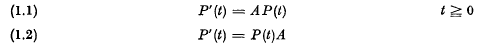
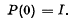
 ) is a set
) is a set 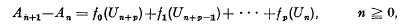
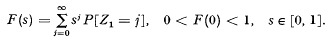
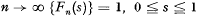 (Harris [1], Chapter 1). In particular, extinction is certain.
(Harris [1], Chapter 1). In particular, extinction is certain.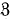 [
[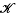 is a family left ideals of
is a family left ideals of 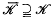 such that all the elements of orders from
such that all the elements of orders from 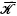 form a submodule in any
form a submodule in any 