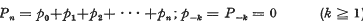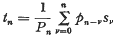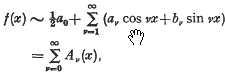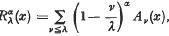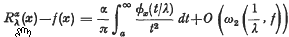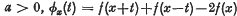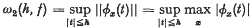Refine search
Actions for selected content:
28894 results in Differential and integral equations, dynamical systems and control theory
Note on Linearly Compact Abelian Groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 433-440
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
A Restricted Inhomogeneous Minimum for Forms
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 363-386
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
On Stone Lattices
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-307
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
ℒ-Realcompactifications and Normal Bases
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 489-495
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
The Lengthening Pendulum
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 331-336
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
Some Remarks on Complete Integral Closure
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 310-314
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
The Compression of Yielding Loops
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 315-330
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
A Note on Separation Axioms Weaker than T1
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-236
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
The Completion of a Lattice Ordered Group
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 182-208
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
Various Ricci Identities in Finsler Space
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 228-232
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
Idempotent-Separating Extensions Of Inverse Semigroups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 211-217
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
JAZ volume 9 issue 1-2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
Semigroups in Which each Ideal is a Retract
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 239-245
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
Monomorphisms, Epimorphisms, and Pull-Backs
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 124-142
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
Note on Finite Topological Spaces
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 252-256
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
Toeplitz Determinants and Szegö's Formula
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 62-99
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
The Iterated Equation of Generalized Axially Symmetric Potential Theory: IV. Circle Theorems
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 153-160
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
On the Absolute Nörlund Summability of a Fourier series (II)1
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 161-166
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
On Single Equational-Axiom Systems for Abelian Groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-152
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
A Note on the Approximation of Continuous Functions by Riesz Typical Means of Their Fourier Series
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 180-181
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
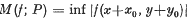
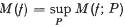

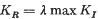
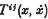 a second order contravariant tensor depending on the element of support
a second order contravariant tensor depending on the element of support 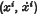 , we have the following theorems.
, we have the following theorems.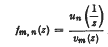
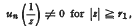
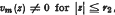

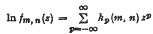
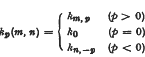
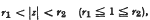
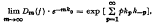
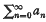 be a given series with its partial sums {S
be a given series with its partial sums {S