Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
On Finite Soluble Groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 250-251
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
Matrix Representations of Inverse Semigroups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 29-61
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
On Properties Possessed by Solvable and Nilpotent Groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 218-227
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
The Terminal Behaviour of a Uniformly Shortening Pendulum
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 246-249
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
On Bare Points
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 25-28
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
Factor Ideals of Some Representation Algebras
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-123
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
Some Uniqueness Theorems for Functional Equations
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 1-2 / February 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 176-179
- Print publication:
- February 1969
-
- Article
-
- You have access
- Export citation
Primitive sequences whose elements have no large prime factors
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 10-15
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
VII.—On the Spectrum of Ordinary Second Order Differential Operators.*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 2 / 1969
- Published online by Cambridge University Press:
- 14 February 2012, pp. 95-119
- Print publication:
- 1969
-
- Article
- Export citation
GMJ volume 10 issue 1 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
Completely injective semigroups with central idempotents
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 16-20
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
Matrices over orthomodular lattices
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 55-59
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
XI.—On Unconditional Convergence in Topological Vector Spaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 2 / 1969
- Published online by Cambridge University Press:
- 14 February 2012, pp. 145-157
- Print publication:
- 1969
-
- Article
- Export citation
On complemented and annihilator algebras
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 38-45
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
XII.—The Hexapole Magnet as a Velocity Selector and Polarizer for Neutral Spin-½ Particles*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 2 / 1969
- Published online by Cambridge University Press:
- 14 February 2012, pp. 158-184
- Print publication:
- 1969
-
- Article
- Export citation
Decreasing Baer semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 46-51
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
On the second natural representation of the symmetric groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 25-37
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
GMJ volume 10 issue 1 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
X.—Determinants for Matrices over Lattices
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 2 / 1969
- Published online by Cambridge University Press:
- 14 February 2012, pp. 138-144
- Print publication:
- 1969
-
- Article
- Export citation
IX.—The Synthesis of 8-Bromo-3-methoxyfluoranthene.*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 2 / 1969
- Published online by Cambridge University Press:
- 14 February 2012, pp. 127-137
- Print publication:
- 1969
-
- Article
- Export citation
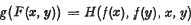
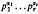 , the
, the