Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
The convergence of Rayleigh-Ritz approximations
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 641-646
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
Non-linear weak shock diffraction
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 737-754
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
Generalized intrinsic form of the characteristic relations in the steady supersonic flow of a gas
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 4 / November 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 647-660
- Print publication:
- November 1968
-
- Article
-
- You have access
- Export citation
Commutative semigroup amalgams
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 609-630
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
JAZ volume 8 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
Corrigendum: Extreme coverings of n-space by spheres
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 638-640
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
The adjoints of differentiable mappings
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 397-409
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
On the product of two linear forms, one homogeneous and one inhomogeneous
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 457-511
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
JAZ volume 8 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
A class of multipliers
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 584-590
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
On the continuity of projections
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 410-414
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
On a sequence of prime numbers
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 571-574
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
Some conformally separable metrics in flat space and their application to accelerated coordinate frameworks in special relativity
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 515-522
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
Solution of Schrödinger equation by Laplace transform
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 557-567
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
A note on free products with a normal amalgamation
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 631-637
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
On the behaviour of the characteristic function of a probability distribution in the neighbourhood of the origin
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 423-443
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
A construction for a self-polar double-N associated with a pair of normal rational curves
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 415-422
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
On the number of varieties of groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 444-446
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
On the Gauss-Green theorem
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-396
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
Fundamental solutions for a class of equations with several singular coefficients
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 575-583
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
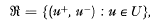
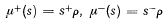
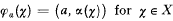
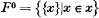 . The terminology will be that of [1].
. The terminology will be that of [1].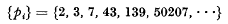
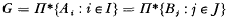
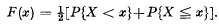
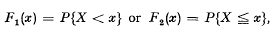
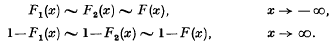
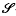 -related”) normal rational curves, in that the spaces
-related”) normal rational curves, in that the spaces 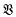 has a finite basis for its laws but some subvariety
has a finite basis for its laws but some subvariety 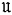 of
of