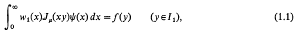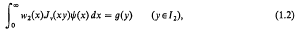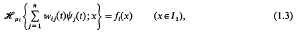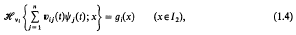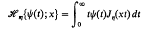Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
A formula for the resolvent of a Reynolds operator
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 447-456
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
Abstract Kernels and Cohomology
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 544-546
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
The automata theory of semigroup embeddings
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 568-570
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
On a family of simple ordered groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 591-608
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
A characterisation of PSL2(Zþλ) and PGL2(Zþλ)
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 523-543
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
The Archimedean property in an ordered semigroup
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 547-556
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
A note on right invariant integrals on locally compact semigroups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 3 / August 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 512-514
- Print publication:
- August 1968
-
- Article
-
- You have access
- Export citation
GMJ volume 9 issue 2 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
On the prime factors of the number 2p-1 - 1
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 83-86
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
A Bessel function inequality connected with stability of least square smoothing, II
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 119-122
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
Weak compactness in locally convex spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 123-127
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
Semiconvex spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 111-118
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
GMJ volume 9 issue 2 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
An algebraically closed field
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 146-151
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
A note on the duality of locally compact groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 87-91
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
Elements of finite order in free product sixth-groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 128-145
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
A characterisation and two examples of Riesz operators
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 106-110
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
Inductive and projective limits of normed spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 103-105
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
An identity for certain Dirichlet series†
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 79-82
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
The solution of certain simultaneous pairs of dual integral equations†
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 2 / July 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 92-102
- Print publication:
- July 1968
-
- Article
-
- You have access
- Export citation
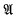 be a complex Banach algebra, possibly non-commutative, with identity
be a complex Banach algebra, possibly non-commutative, with identity 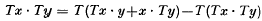
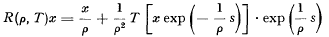
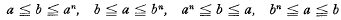
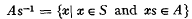
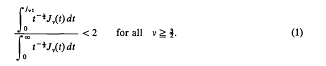
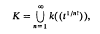
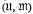 of spaces
of spaces 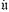 and maps
and maps 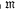 is a space
is a space 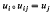 whenever
whenever 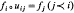 then there is a unique map
then there is a unique map