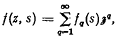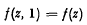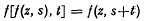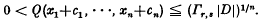Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
Error analysis of an algorithm for summing certain finite series
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 213-221
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Coordinate and momentum representations in quantum mechanics
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 304-309
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
On an integral involving the H-function
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 373-376
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Characteristic multipliers and stationary integrals
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 377-382
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Positive values of inhomogeneous quaternary ouadratic forms, II
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-303
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Primitive homomorphic images of semigroups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 350-354
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
On the Equation ax—xb = c
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 383-384
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Alternative derivation of some regular continued fractions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 205-212
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Two problems on finite groups with k conjugate classes
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 49-55
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
An existence theorem for optimal stochastic programming
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 114-118
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
A note on compactifications and semi-normal spaces
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 102-108
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
Transitivity in integral symplectic forms
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 43-48
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
A sufficient condition for an extreme covering of n-space by spheres
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 56-62
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
Harris Charles Levey
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-5
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
The square root of a positive self-adjoint operator
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-36
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
Statistics of fragments from enzyme-induced breakup of co-polymer chains
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 63-86
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
Corrigendum: On metabelian p-groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, p. 128
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
A non-embeddable composite of embeddable functions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-113
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
JAZ volume 8 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
Positive values of inhomogeneous quaternary quadratic forms, I
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 87-101
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
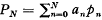 , where the coefficients
, where the coefficients 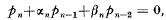
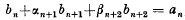
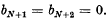
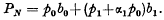
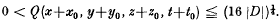
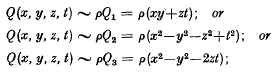

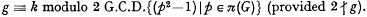
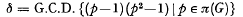
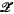 for the closed sets of a space
for the closed sets of a space