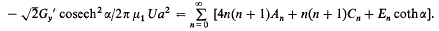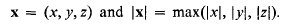Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
V—The Brownian Movement of a One-Dimensional Non-Harmonic Oscillator
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 1 / 1968
- Published online by Cambridge University Press:
- 14 February 2012, pp. 70-82
- Print publication:
- 1968
-
- Article
- Export citation
On the selection of non-σ-finite subsets
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-164
- Print publication:
- December 1967
-
- Article
- Export citation
On the finite deformation of inhomogeneous elastic materials
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 215-219
- Print publication:
- December 1967
-
- Article
- Export citation
Combinatorially regular polytopes
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-150
- Print publication:
- December 1967
-
- Article
- Export citation
Index to volume 14
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, p. 233
- Print publication:
- December 1967
-
- Article
- Export citation
Varieties representing certain systems of Schubert triangles
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-160
- Print publication:
- December 1967
-
- Article
- Export citation
Simultaneous asymptotic Diophantine approximations
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 173-180
- Print publication:
- December 1967
-
- Article
- Export citation
The connectivity function of a graph
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 197-202
- Print publication:
- December 1967
-
- Article
- Export citation
Linear forms in the logarithms of algebraic numbers (III)
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 220-228
- Print publication:
- December 1967
-
- Article
- Export citation
MTK volume 14 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1967
-
- Article
-
- You have access
- Export citation
Coefficient regions for univalent polynomials of small degree
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 165-169
- Print publication:
- December 1967
-
- Article
- Export citation
On the units of algebraic number fields
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 121-124
- Print publication:
- December 1967
-
- Article
- Export citation
Double covering with spheres
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 207-214
- Print publication:
- December 1967
-
- Article
- Export citation
A slow motion of viscous liquid caused by a slowly moving solid sphere: an addendum
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 170-172
- Print publication:
- December 1967
-
- Article
- Export citation
On the realization of distances within coverings of an n-sphere
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 203-206
- Print publication:
- December 1967
-
- Article
- Export citation
On addition theorems for spheroidal harmonics with some applications
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 132-141
- Print publication:
- December 1967
-
- Article
- Export citation
A shearing motion of viscous liquid
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-131
- Print publication:
- December 1967
-
- Article
- Export citation
Some Diophantine equations in three variables with only finitely many solutions
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-120
- Print publication:
- December 1967
-
- Article
- Export citation
Polynomials with multiple zeros
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 181-196
- Print publication:
- December 1967
-
- Article
- Export citation
Corrigendum and addendum
-
- Journal:
- Mathematika / Volume 14 / Issue 2 / December 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-232
- Print publication:
- December 1967
-
- Article
- Export citation
 of each particle
of each particle  (Grünbaum [
(Grünbaum [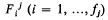 be its
be its 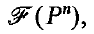 partially ordered by inclusion ([
partially ordered by inclusion ([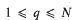
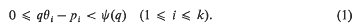
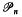 be the class of normalised polynomials of the form:
be the class of normalised polynomials of the form: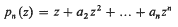
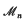 be the class of “polynomials” of the form
be the class of “polynomials” of the form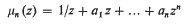
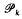 (
(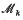 (
(