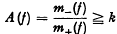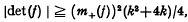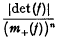Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
On Riemann surfaces with maximal automorphism groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 2 / July 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 102-112
- Print publication:
- July 1967
-
- Article
-
- You have access
- Export citation
On the nonexistence of Lp solutions of certain nonlinear differential equations
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 2 / July 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 133-138
- Print publication:
- July 1967
-
- Article
-
- You have access
- Export citation
On maximal nilpotent subrings of right Noetherian rings
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 2 / July 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 89-101
- Print publication:
- July 1967
-
- Article
-
- You have access
- Export citation
The distribution of the residues of a quartic polynomial
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 2 / July 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 67-88
- Print publication:
- July 1967
-
- Article
-
- You have access
- Export citation
Nul solutions of the Kolmogorov differential equations
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 56-61
- Print publication:
- June 1967
-
- Article
- Export citation
On the Hankel determinants of univalent functions
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 108-112
- Print publication:
- June 1967
-
- Article
- Export citation
Classnumbers and unit signatures
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 94-98
- Print publication:
- June 1967
-
- Article
- Export citation
On the zeros of Epstein's zeta function
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 47-55
- Print publication:
- June 1967
-
- Article
- Export citation
Slow motion of an incompressible viscous liquid generated by the rotation of two spheres in contact
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 43-46
- Print publication:
- June 1967
-
- Article
- Export citation
The determination of convex bodies from their mean radius of curvature functions
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-13
- Print publication:
- June 1967
-
- Article
- Export citation
Uniqueness theorems for linearized theories of interacting continua
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 27-42
- Print publication:
- June 1967
-
- Article
- Export citation
On the existence of non-atomic measures
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 62-67
- Print publication:
- June 1967
-
- Article
- Export citation
On the power free values of polynomials
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 21-26
- Print publication:
- June 1967
-
- Article
- Export citation
The large sieve
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-20
- Print publication:
- June 1967
-
- Article
- Export citation
A note on successive approximation
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-101
- Print publication:
- June 1967
-
- Article
- Export citation
MTK volume 14 issue 1 Cover and Front matter
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- June 1967
-
- Article
-
- You have access
- Export citation
Linear forms in the logarithms of algebraic numbers (II)
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-107
- Print publication:
- June 1967
-
- Article
- Export citation
Supersonic flow and wing-body interference
-
- Journal:
- Mathematika / Volume 14 / Issue 1 / June 1967
- Published online by Cambridge University Press:
- 26 February 2010, pp. 68-93
- Print publication:
- June 1967
-
- Article
- Export citation
Minimum determinant of asymmetric quadratic forms
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 2 / May 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 177-190
- Print publication:
- May 1967
-
- Article
-
- You have access
- Export citation
A characterization of lattice-ordered groups by their convex L-subgroups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 2 / May 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 145-159
- Print publication:
- May 1967
-
- Article
-
- You have access
- Export citation


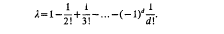
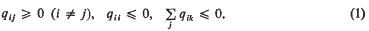
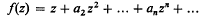
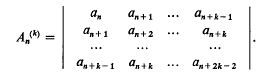
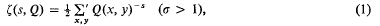
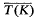 of
of 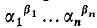 is transcendental.
is transcendental.