Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
The Fitting subgroup of a linear solvable group
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 417-424
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
Relativity, uncertainty and electrodynamics
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 513-523
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
Some local limit results in fluctuation theory
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 455-464
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
Some properties of locally compact groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 433-454
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
Trivial knots with arbitrary projection
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 481-489
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
A third-Engel 5-group
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 555-569
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
The extreme coverings of 4-space by spheres
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 490-496
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
On the height of trees
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 497-507
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
A note on the independence of the axioms for a vector space
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-428
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
Sequences of integers satisfying congruence relations and Pisot-Vijayaraghavan numbers
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 508-512
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
A note on de Sitter type solutions of Einstein's field equations
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 429-432
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
On the transient behaviour of a Poisson branching process
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 465-480
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
JAZ volume 7 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
Semigroup structures for families of functions, III:
-Semigroups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 524-538
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
Normal p-subgroups of solvable linear groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 545-551
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
JAZ volume 7 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
The approximation of continuous functions by Riesz typical means of their Fourier series
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 539-544
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
On radical extensions of rings
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 552-554
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
Finite groups with a self-centralizing subgroup of order 4
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 4 / November 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 570-576
- Print publication:
- November 1967
-
- Article
-
- You have access
- Export citation
Finitely generated
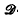 -groups
-groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 375-409
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
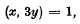
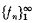 of positive integers having exponential growth:
of positive integers having exponential growth: 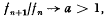 and becoming ultimately periodic modulo each member of a rather sparse infinite set of integers. If sufficient, natural conditions are placed on the growth and periodicities of
and becoming ultimately periodic modulo each member of a rather sparse infinite set of integers. If sufficient, natural conditions are placed on the growth and periodicities of 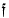 be a function mapping
be a function mapping 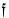 (
( -groups
-groups
