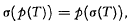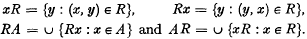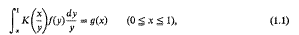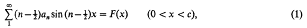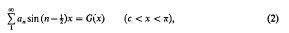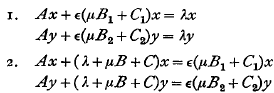Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
The relativistic incompressible sphere
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 6-16
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
JAZ volume 8 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
An unbounded spectral mapping theorem
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 119-127
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
Relations on topological spaces: Urysohn's lemma
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 37-42
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
IV.—On the Integrals of Hua and James.*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 1 / 1968
- Published online by Cambridge University Press:
- 14 February 2012, pp. 54-69
- Print publication:
- 1968
-
- Article
- Export citation
PRM volume 68 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 1 / 1968
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1968
-
- Article
-
- You have access
- Export citation
Type Radicals
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 1 / January 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 22-29
- Print publication:
- January 1968
-
- Article
-
- You have access
- Export citation
Translational hull and semigroups of binary relations
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 1 / January 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 12-21
- Print publication:
- January 1968
-
- Article
-
- You have access
- Export citation
II.—The Attempted Synthesis of Benzo[a]biphenylene
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 1 / 1968
- Published online by Cambridge University Press:
- 14 February 2012, pp. 23-29
- Print publication:
- 1968
-
- Article
- Export citation
The torsion of a semi-infinite elastic solid by an elliptical stamp
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 1 / January 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 36-45
- Print publication:
- January 1968
-
- Article
-
- You have access
- Export citation
GMJ volume 9 issue 1 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 1 / January 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1968
-
- Article
-
- You have access
- Export citation
A Sceptical Chemist in a Biological Wonderland
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 1 / 1968
- Published online by Cambridge University Press:
- 14 February 2012, pp. 1-22
- Print publication:
- 1968
-
- Article
- Export citation
GMJ volume 9 issue 1 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 1 / January 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f6
- Print publication:
- January 1968
-
- Article
-
- You have access
- Export citation
The translational hull of a completely 0-simple semigroup
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 1 / January 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-11
- Print publication:
- January 1968
-
- Article
-
- You have access
- Export citation
A procedure for deriving inversion formulae for integral transform pairs of a general kind
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 1 / January 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 67-77
- Print publication:
- January 1968
-
- Article
-
- You have access
- Export citation
PRM volume 68 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 1 / 1968
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1968
-
- Article
-
- You have access
- Export citation
Regular ω-semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 1 / January 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 46-66
- Print publication:
- January 1968
-
- Article
-
- You have access
- Export citation
Note on a pair of dual trigonometric series
-
- Journal:
- Glasgow Mathematical Journal / Volume 9 / Issue 1 / January 1968
- Published online by Cambridge University Press:
- 18 May 2009, pp. 30-35
- Print publication:
- January 1968
-
- Article
-
- You have access
- Export citation
III.—Multiplicative Ideal Theory and Rings of Quotients. I.*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 1 / 1968
- Published online by Cambridge University Press:
- 14 February 2012, pp. 30-53
- Print publication:
- 1968
-
- Article
- Export citation
VI.—On Solvability of Some Two-Parameter Eigenvalue Problems in Hilbert Space
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 1 / 1968
- Published online by Cambridge University Press:
- 14 February 2012, pp. 83-93
- Print publication:
- 1968
-
- Article
- Export citation