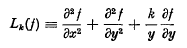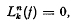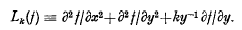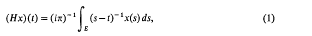Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
The iterated equation of generalized axially symmetric potential theory. II. General solutions of Weinstein's type
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 277-289
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
JAZ volume 7 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
An Md-class of sets indexed by a regressive function
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-310
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
Functions over the residue field modulo a prime
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 410-416
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
A Helly-type theorem on a sphere
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 323-326
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
JAZ volume 7 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
Certain homomorphisms of a compact semigroup onto a thread
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 311-322
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
Approximation in algebraic function fields of one variable
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 341-355
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
Verbal wreath products and certain product varieties of groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 356-374
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
Report of the Australian Mathematical Society
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, p. 257
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
The field structure of the real number system
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-262
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
Semigroups acting on continua
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-340
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
The iterated equation of generalized axially symmetric potential theory. I. Particular solutions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 263-276
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
The iterated equation of generalized axially symmetric potential theory. III. Conjugate general solutions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 3 / August 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 290-300
- Print publication:
- August 1967
-
- Article
-
- You have access
- Export citation
On products of idempotent matrices
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 2 / July 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 118-122
- Print publication:
- July 1967
-
- Article
-
- You have access
- Export citation
GMJ volume 8 issue 2 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 2 / July 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- July 1967
-
- Article
-
- You have access
- Export citation
On Schur's second partition theorem
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 2 / July 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 127-132
- Print publication:
- July 1967
-
- Article
-
- You have access
- Export citation
Hilbert transforms and unitary equivalence
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 2 / July 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 113-117
- Print publication:
- July 1967
-
- Article
-
- You have access
- Export citation
GMJ volume 8 issue 2 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 2 / July 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- July 1967
-
- Article
-
- You have access
- Export citation
Some results on coherent rings II
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 2 / July 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 123-126
- Print publication:
- July 1967
-
- Article
-
- You have access
- Export citation
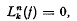
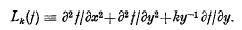
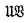 is generated by a finite group if and only if
is generated by a finite group if and only if 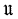 is nilpotent,
is nilpotent, 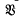 is abelian, and the exponents of
is abelian, and the exponents of