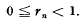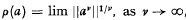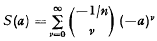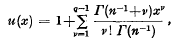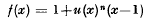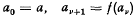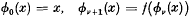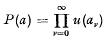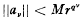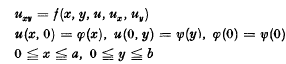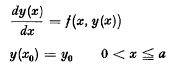Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
Embedding semirings in semirings with multiplicative unit
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-191
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Completion in the bidual
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 238-241
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
A note on approximation by automorphic images of functions in L1 and L∞
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 222-230
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Kinematic geometry; an axiomatic system for Minkowski space-time: M. L. Urquhart in Memoriam
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 134-160
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
A note on the Ritz method with an application to overtone stellar pulsation theory
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 275-286
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Damping loss in a cascade of fluttering phased aerofoils
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-344
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Certain topological semirings in R1
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-182
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
A further generalization of the arc-sine law
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-372
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Unbiased distinguishing of translation families and integrability with respect to a convolution of measures
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-204
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
JAZ volume 8 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Products of abelian hopfian groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 322-326
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
On the number of topologies definable for a finite set
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 194-198
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
M. L. Urquhart
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-133
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
The order topology in a bicompactly generated lattice
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-349
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
An unsolved problem on the powers of 3/2*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 313-321
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
On dams of finite capacity
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 161-170
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
A note on the propagation of plane waves in elastic and plastic solids
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 231-237
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Infinite product expansions for matrix n-th roots
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 242-249
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
JAZ volume 8 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
Cubature method for the numerical solution of the characteristic initial value problem: uxy = f(x, y, u, ux, Uy)
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 2 / May 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 355-368
- Print publication:
- May 1968
-
- Article
-
- You have access
- Export citation
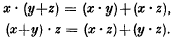
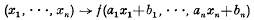
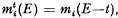 , where
, where 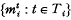 , where
, where 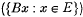 with
with 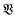
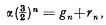
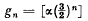
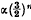 , i.e the integral part of
, i.e the integral part of