Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
The order problem and the power problem for free product sixth-groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-9
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
The numerical range of an element of a normed algebra
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 68-72
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
Remark on a criterion for common transversals
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 66-67
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
The evaluation functionals associated with an algebra of bounded operators
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 73-76
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
Residuation theory and matrix multiplication on orthomodular lattices
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 60-65
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
PRM volume 68 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 2 / 1969
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1969
-
- Article
-
- You have access
- Export citation
VIII.—Some 9-Fluorenyl and 9,9′-Bifluorenyl Derivatives.*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 2 / 1969
- Published online by Cambridge University Press:
- 14 February 2012, pp. 120-126
- Print publication:
- 1969
-
- Article
- Export citation
Certain congruence and quotient lattices related to completely 0-simple and primitive regular semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 21-24
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
PRM volume 68 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 68 / Issue 2 / 1969
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1969
-
- Article
-
- You have access
- Export citation
Simple proof of a theorem on permanents
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 52-54
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
Martingale convergence theorems for sequences of Stone algebras
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 1 / January 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 77-83
- Print publication:
- January 1969
-
- Article
-
- You have access
- Export citation
On partitioning ordered sets into cofinal subsets
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 217-222
- Print publication:
- December 1968
-
- Article
- Export citation
The large sieve inequality for algebraic number fields
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 178-187
- Print publication:
- December 1968
-
- Article
- Export citation
Decomposition of functions whose partial derivatives are measures
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 149-152
- Print publication:
- December 1968
-
- Article
- Export citation
Some applications of a theorem of Rado
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 199-203
- Print publication:
- December 1968
-
- Article
- Export citation
Artin's conjecture on the average
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 223-226
- Print publication:
- December 1968
-
- Article
- Export citation
A presentation of SL2 for Euclidean imaginary quadratic number fields
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 156-163
- Print publication:
- December 1968
-
- Article
- Export citation
Index to volume 15
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, p. 228
- Print publication:
- December 1968
-
- Article
- Export citation
Diagrams for centrally symmetric polytopes
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 123-138
- Print publication:
- December 1968
-
- Article
- Export citation
On the group of automorphisms of the Euclidean hypersphere
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 193-198
- Print publication:
- December 1968
-
- Article
- Export citation
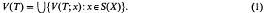
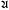 = (
= (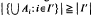
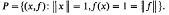
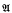 of
of 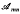 will denote the set of all
will denote the set of all 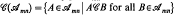 , where we say that
, where we say that 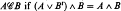 . In § 1 it is shown that mappings from
. In § 1 it is shown that mappings from 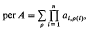
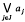 and the greatest lower bound by
and the greatest lower bound by 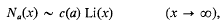
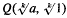 .
.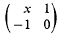 as
as 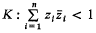 be the unit hypersphere. Further, let
be the unit hypersphere. Further, let 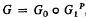 , where
, where 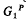 is a 2
is a 2