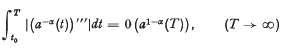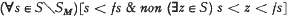Refine search
Actions for selected content:
28894 results in Differential and integral equations, dynamical systems and control theory
Commutative Banach Algebras with Idempotent Maximal Ideals
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 275-286
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
On Characteristic Morphisms: In Memoriam Thomas Macfarland Cherry
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 478-488
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
Some Classes of Indecomposable Varieties of Groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 387-398
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
Some Results on ω-Derivatives and BV-ω Functions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-360
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
Automorphisms of Finite Groups and their Fixed-Point Groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 467-477
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
On Schoenberg's Rational Polygon Problem
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 337-344
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
Stone algebras form an equational class: (Remarks on Lattice Theory III)
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 308-309
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
A Remark on Critical Groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 465-466
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
An Upper Bound for Volumes of Convex Bodies
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 503-510
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
Congruences on ωn-Bisimple Semigroups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-274
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
Remarks on Stability Conditions for the Differential Equation x″ + a(t)ƒ(x) = 01
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 496-502
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
A Theorem on Partially Ordered Sets and its Application
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 361-362
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
Some Finite Nilpotent p-Groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-288
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
JAZ volume 9 issue 3-4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
Some Remarks on a Class of Distributive Lattices
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-296
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
Spherical Modifications and the Strong Category of Manifolds
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 449-454
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
JAZ volume 9 issue 3-4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
A Note on Finite-Dimensional Differentiable Mappings
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-408
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
On Diagrams of Vector Spaces
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 445-448
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
Multipliers between Some Spaces of Distributions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 9 / Issue 3-4 / May 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 415-423
- Print publication:
- May 1969
-
- Article
-
- You have access
- Export citation
 be a commutative Banach algebra over the complex field
be a commutative Banach algebra over the complex field  and
and 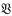 are varieties, then
are varieties, then 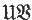 is the class of all groups
is the class of all groups  the variety generated by the unit group, and by
the variety generated by the unit group, and by 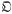 the variety of all groups. We say that a variety
the variety of all groups. We say that a variety  , and
, and 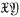 , with both
, with both 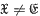 and
and 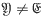 One of the basic results in the theory of varieties of groups is that the set of varieties, excluding
One of the basic results in the theory of varieties of groups is that the set of varieties, excluding 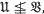


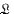 = 〈
= 〈
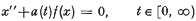
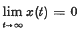
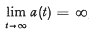
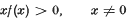
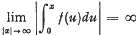
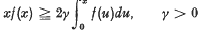
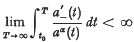
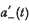 = max (−
= max (−