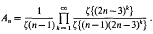Refine search
Actions for selected content:
28894 results in Differential and integral equations, dynamical systems and control theory
Two problems in singular perturbations of differential equations
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 1-2 / August 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-50
- Print publication:
- August 1969
-
- Article
-
- You have access
- Export citation
A class of c-groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 1-2 / August 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 182-184
- Print publication:
- August 1969
-
- Article
-
- You have access
- Export citation
Non-existence of a certain projective plane
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 1-2 / August 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 214-218
- Print publication:
- August 1969
-
- Article
-
- You have access
- Export citation
The Riemann surface of a ring
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 1-2 / August 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 251-256
- Print publication:
- August 1969
-
- Article
-
- You have access
- Export citation
A Hahn-Banach theorem for semifields
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 1-2 / August 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 20-22
- Print publication:
- August 1969
-
- Article
-
- You have access
- Export citation
Remarks on the asymptotic behaviour of perturbed linear systems†
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 116-120
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
Radicals of semigroup rings†
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 85-93
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
A covering theorem for typically real functions
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 153-155
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
Lattice subgroups of free congruence groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 106-115
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
Semiconvex spaces II
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 103-105
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
A variance method in combinatorial number theory
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 126-129
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
 -injectors of locally soluble FC-groups
-injectors of locally soluble FC-groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 130-136
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
On the loci |f(z)| = R, f(z) Entire
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 94-102
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
GMJ volume 10 issue 2 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
The inversion of Hankel transforms of order zero and unity
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 156-161
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
Some triple trigonometrical series
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 121-125
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
An elementary inequality in function theory
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 162-168
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
GMJ volume 10 issue 2 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
A note on the thermoelastic problem for a penny-shaped crack
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 169-172
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
Sets of integers containing no n terms in geometric progression
-
- Journal:
- Glasgow Mathematical Journal / Volume 10 / Issue 2 / July 1969
- Published online by Cambridge University Press:
- 18 May 2009, pp. 137-146
- Print publication:
- July 1969
-
- Article
-
- You have access
- Export citation
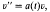
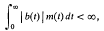
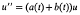
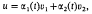
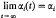
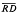 denote the contracted semigroup ring of the ompletely 0-simple semigroup
denote the contracted semigroup ring of the ompletely 0-simple semigroup 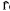 (1) be the inhomogeneous modular group of 2 × 2 integral matrices of determinant 1 in which a matrix is identified with its negative.
(1) be the inhomogeneous modular group of 2 × 2 integral matrices of determinant 1 in which a matrix is identified with its negative. 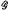 of
of 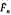 of rank
of rank 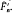 . In particular, he showed that, if
. In particular, he showed that, if 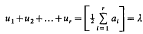
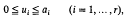
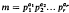 which contain exactly λ prime factors counted according to multiplicity, and is therefore, as is proved in [1], the cardinality of the largest possible set of divisors of
which contain exactly λ prime factors counted according to multiplicity, and is therefore, as is proved in [1], the cardinality of the largest possible set of divisors of 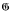 -injectors of locally soluble
-injectors of locally soluble