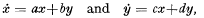Refine search
Actions for selected content:
28894 results in Differential and integral equations, dynamical systems and control theory
Stability of a pair of first order linear differential equations
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 283-298
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
On some Schreier varieties of universal algebras: To Bernhard hermann Neumann on his 60th birthday
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 442-444
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
Modular representations of C2×C2
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 363-366
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
Residual finiteness of permutational products
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 423-428
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
Lattice isomorphic solvable Lie algebras
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 266-268
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
JAZ volume 10 issue 3-4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
Electrochemical dissolution of an anode
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 414-422
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
Decomposition of representation algebras
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 395-402
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
Commutator subgroups of finite p-groups: To Bernhard Hermann Neumann on his 60th birthday
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 480-484
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
Some results using general moment functions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 429-441
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
The Hughes Problem and others: To Bernhard Hermann Neumann on his 60th birthday
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 475-479
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
A faithful matrix representation for certain centre-y-metabelian groups: To Bernhard Hermann Neumann on his 60th birthday
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 451-464
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
Meromorphic functions with one deficient value
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 3-4 / November 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 355-358
- Print publication:
- November 1969
-
- Article
-
- You have access
- Export citation
A Characterization of the finite simple group U4(3)
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 1-2 / August 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 77-94
- Print publication:
- August 1969
-
- Article
-
- You have access
- Export citation
JAZ volume 10 issue 1-2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 1-2 / August 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- August 1969
-
- Article
-
- You have access
- Export citation
On the finite similarity groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 1-2 / August 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 106-110
- Print publication:
- August 1969
-
- Article
-
- You have access
- Export citation
Derivation of a general lorentz transformation without rotation
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 1-2 / August 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 141-144
- Print publication:
- August 1969
-
- Article
-
- You have access
- Export citation
JAZ volume 10 issue 1-2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 1-2 / August 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- August 1969
-
- Article
-
- You have access
- Export citation
Semigroups with few endomorphisms: In Memoriam Anatoli Ivanovič Mal'cev
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 1-2 / August 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 162-168
- Print publication:
- August 1969
-
- Article
-
- You have access
- Export citation
A note on the intersection of free maximal ideals
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 10 / Issue 1-2 / August 1969
- Published online by Cambridge University Press:
- 09 April 2009, pp. 204-206
- Print publication:
- August 1969
-
- Article
-
- You have access
- Export citation