Problems associated with m-ary trees have been studied by computer scientists and combinatorialists. It is well known that a simple generalization of the Catalan numbers counts the number of m-ary trees on n nodes. In this paper we consider τm, n, the number of m-ary search trees on n keys, a quantity that arises in studying the space of m-ary search trees under the uniform probability model. We prove an exact formula for τm, n, both by analytic and by combinatorial means. We use uniform local approximations for sums of i.i.d. random variables to study the asymptotic development of τm, n for fixed m as n→∞.

The Turán Number T(n, k, r) is the smallest possible number of edges in a k-graph of ordern such that every set of r vertices contains an edge. The limit

formula here

exists, but there is no pair (k, r) with r>k[ges ]3 for which this function could be determined as yet. We give a constructive proof of the upper bound

formula here

for every k and r with r[ges ]k[ges ]2. In the case k=6, r=11 we improve this result, refuting thereby a conjecture of Turán.

In this paper the method of inner and outer sums [5], together with the computational power of computer symbolic manipulation, are used to extend to high order the asymptotic expansions in an appropriate limit of some infinite series arising in low Reynolds-number fluid mechanics. The enhanced applicability of the expansions is demonstrated, and the method is extended to treat alternating series.

The forms under discussion are integral positive definite quadratic forms in three variables. Such a form g is called regular if g represents every integer represented by the genus of g. This can be recast in elementary terms: g is regular if the solvability of g≡a (mod n) for every n implies the solvability of g = a.

The maximal zero-free intervals for chromatic polynomials of graphs are precisely (−∞, 0), (0, 1), (1, 32/27]. We also investigate the distribution of zeros of chromatic polynomials in various classes of graphs closed under minors. For example, the zeros of chromatic polynomials of graphs of tree-width at most k consist of 0, 1 and a dense subset of the interval (32/27, k].

A graph G is called an H-type graph for some graph H if there is a mapping from V(G) to V(H) preserving edges. In this paper, we shall prove that: (1) every triangle-free graph G of order n with χ(G)[les ]3 and δ(G)>n/3 is of Fd-type for some d[ges ]1, where Fd is a certain d-regular triangle-free Hamiltonian Cayley graph of order 3d−1, (2) every triangle-free graph G of order n with χ(G)[ges ]4 and δ(G)>n/3 contains the Mycielski graph (see Figure 2) as a subgraph.

Rabinowitz' global bifurcation theorem shows that for a large class of nonlinear eigenvalue problems a continuum (i.e., a closed, connected set) of solutions bifurcates from the trivial solution at each eigenvalue (or characteristic value) of odd multiplicity of the linearized problem (linearized at the trivial solution). Each continuum must either be unbounded, or must meet some other eigenvalue. This paper considers a class of such nonlinear eigenvalue problems having simple eigenvalues and a “weak” nonlinear term. A result regarding the location of the continua is obtained which shows, in particular, that in this case the bifurcating continua must be unbounded. Also, under further differentiability conditions it is shown that the continua are smooth, 1-dimensional curves and that there are no non-trivial solutions of the equation other than those lying on the bifurcating continua.

The cyclic tour property has previously been an equality for the expected time to complete a tour, compared with that for the reverse tour, for reversible Markov chains. We give a simple bijection to show that the equality can be extended to the distributions involved. The bijection is based on rotation of circular words.

A long time ago Ju. E. Vapne ([2], [3]) and, independently, the author ([4], [5]) classified those standard and complete wreath products that have faithful representations of finite degree over (commutative) fields. See [6] pages 37 40 & 150–154 for an account of this. Recently, in connection with finitary linear groups, I needed a more general wreath product. Somewhat to my surprise neither the classification nor the proof for these generalized wreath products was a straightforward translation from the standard case. The situation is intrinsically more complex and it seems worthwhile recording it separately.

We study the fraction of time that a Markov chain spends in a given subset of states. We give an exponential bound on the probability that it exceeds its expectation by a constant factor. Our bound depends on the mixing properties of the chain, and is asymptotically optimal for a certain class of Markov chains. It beats the best previously known results in this direction. We present an application to the leader election problem.

In [CKR], Chan, Kim and Raghavan determine all universal positive ternary integral quadratic forms over real quadratic number fields. In this context, universal means that the form represents all totally positive elements of the ring of integers of the underlying field. This generalizes the usage of the term introduced by Dickson for the case of the ring of rational integers [D]. In the present paper, we will continue the investigation of quadratic forms with this property, considering positive quaternary forms over totally real number fields. The main goal of the paper is to prove that if E is a totally real number field of odd degree over the field of rational numbers, then there are at most finitely many inequivalent universal positive quaternary quadratic forms over the ring of integers of E. In fact, the stronger result will be proved that this finiteness holds for those forms which represent all totally positive multiples of any fixed totally positive integer. The necessity of the assumption of oddness of the degree of the extension for a general result of this type can be seen from the existence of universal ternary forms over certain real quadratic fields (for example, the sum of three squares over the field ℚ(√5), as first shown by Maass [M]).

We investigate the distribution of the hitting time T defined by the first visit of the Brownian motion on the Sierpiński gasket at geodesic distance r from the origin. For this purpose we perform a precise analysis of the moment generating function of the random variable T. The key result is an explicit description of the analytic behaviour of the Laplace- Stieltjes transform of the distribution function of T. This yields a series expansion for the distribution function and the asymptotics for t →0.

For a fixed integer k ≥ 2 suppose we have functions Li (x) satisfying the following conditions.

Ramanujan's work on the asymptotic behaviour of the hypergeometric function has been recently refined to the zero-balanced Gaussian hypergeometric function F(a, b; a + b; x) as x→1.We extend these results for F(a, b; c; x) when a, b, c>0 and c<a + b.

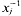For i = 1,…, n let ai be a homogeneous polynomial of degree ri(>0) in the graded polynomial ring R[x1, …, xm], or R[x] for short, where R is a commutative ring with unity and x1, …, xm are indeterminates of degree 1. Let of degree - 1 be a formal inverse of 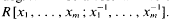xj and let U denote the graded R[x]-module In [2, §2] we introduced a graded complex of r-modules.

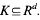A random polytope, Kn, is the convex hull of n points chosen randomly, independently, and uniformly from a convex body It is shown here that, with high probability, Kn can be obtained by taking the convex hull of m = o(n) points chosen independently and uniformly from a small neighbourhood of the boundary of K.

We show that a measure on ℝd is linearly rectifiable if, and only if, the lower l-density is positive and finite and agrees with the lower average l-density almost everywhere.