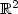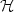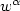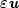Refine search
Actions for selected content:
6997 results in Mathematical modeling and methods
ERROR ESTIMATES FOR DOMINICI’S HERMITE FUNCTION ASYMPTOTIC FORMULA AND SOME APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 04 December 2009, pp. 550-561
-
- Article
-
- You have access
- Export citation
A VALUATION FORMULA FOR MULTI-ASSET, MULTI-PERIOD BINARIES IN A BLACK–SCHOLES ECONOMY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 04 December 2009, pp. 475-485
-
- Article
-
- You have access
- Export citation
ANALYSIS OF BLOCK-SOR ITERATION FOR THE THREE-DIMENSIONAL LAPLACIAN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 04 December 2009, pp. 501-512
-
- Article
-
- You have access
- Export citation
The H –1-norm of tubular neighbourhoods of curves
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 04 December 2009, pp. 131-154
- Print publication:
- January 2011
-
- Article
- Export citation
UNSTEADY BOUNDARY LAYERS: CONVECTIVE HEAT TRANSFER OVER A VERTICAL FLAT PLATE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 04 December 2009, pp. 541-549
-
- Article
-
- You have access
- Export citation
ANZ volume 50 issue 4 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 04 December 2009, pp. b1-b9
-
- Article
-
- You have access
- Export citation
Erratum of “The squares of the Laplacian-Dirichlet eigenfunctions are generically linearly independent”
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 04 December 2009, pp. 806-807
- Print publication:
- July 2010
-
- Article
- Export citation
REFLECTED BACKWARD STOCHASTIC DIFFERENTIAL EQUATIONS DRIVEN BY A LÉVY PROCESS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 04 December 2009, pp. 486-500
-
- Article
-
- You have access
- Export citation

The Matrix Analysis of Vibration
-
- Published online:
- 24 November 2009
- Print publication:
- 31 May 1979
PRACTICAL RUNGE–KUTTA METHODS FOR SCIENTIFIC COMPUTATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 333-342
-
- Article
-
- You have access
- Export citation
COMPONENTS AND PHASES: MODELLING PROGRESSIVE HYDROTHERMAL ERUPTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 365-380
-
- Article
-
- You have access
- Export citation
MODELLING SEA ICE GROWTH
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 306-319
-
- Article
-
- You have access
- Export citation
ANZ volume 50 issue 3 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
RECONSIDERING TRIGONOMETRIC INTEGRATORS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 320-332
-
- Article
-
- You have access
- Export citation
A CONCEPTUAL MODEL FOR THE ORIGINS OF GEOTHERMAL AND VOLCANIC ACTIVITY IN THE NORTH ISLAND OF NEW ZEALAND
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 421-425
-
- Article
-
- You have access
- Export citation
Weighted regularization for composite materialsin electromagnetism
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 03 November 2009, pp. 75-108
- Print publication:
- January 2010
-
- Article
- Export citation
EFFECTIVE SLIP LENGTH OF NANOSCALE MIXED-SLIP SURFACES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 381-394
-
- Article
-
- You have access
- Export citation
ORTHOGONAL FUNCTIONS AND ZERNIKE POLYNOMIALS—A RANDOM VARIABLE INTERPRETATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 435-444
-
- Article
-
- You have access
- Export citation
ANZ volume 50 issue 3 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
A MODEL OF ION TRANSPORT IN CONJUGATED POLYMERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 355-364
-
- Article
-
- You have access
- Export citation