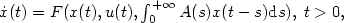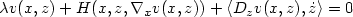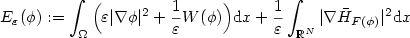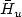Refine search
Actions for selected content:
6997 results in Mathematical modeling and methods
Hamilton-Jacobi-Bellman equations for the optimal control of a state equation with memory
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 31 July 2009, pp. 744-763
- Print publication:
- July 2010
-
- Article
- Export citation
Index of Examples
-
- Book:
- Elementary Probability for Applications
- Published online:
- 05 June 2012
- Print publication:
- 31 July 2009, pp 241-241
-
- Chapter
- Export citation
1 - Basic Concepts
-
- Book:
- Elementary Probability for Applications
- Published online:
- 05 June 2012
- Print publication:
- 31 July 2009, pp 1-31
-
- Chapter
- Export citation
2 - Combinatorial Probability
-
- Book:
- Elementary Probability for Applications
- Published online:
- 05 June 2012
- Print publication:
- 31 July 2009, pp 32-80
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Elementary Probability for Applications
- Published online:
- 05 June 2012
- Print publication:
- 31 July 2009, pp i-iv
-
- Chapter
- Export citation
Preface
-
- Book:
- Elementary Probability for Applications
- Published online:
- 05 June 2012
- Print publication:
- 31 July 2009, pp vii-x
-
- Chapter
- Export citation
7 - Option Pricing
-
- Book:
- Elementary Probability for Applications
- Published online:
- 05 June 2012
- Print publication:
- 31 July 2009, pp 229-236
-
- Chapter
- Export citation
Index of Terms
-
- Book:
- Elementary Probability for Applications
- Published online:
- 05 June 2012
- Print publication:
- 31 July 2009, pp 239-240
-
- Chapter
- Export citation
Normal Table
-
- Book:
- Elementary Probability for Applications
- Published online:
- 05 June 2012
- Print publication:
- 31 July 2009, pp 237-238
-
- Chapter
- Export citation
On the ersatz material approximation in level-set methods
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 31 July 2009, pp. 618-634
- Print publication:
- July 2010
-
- Article
- Export citation
6 - Limit Theorems
-
- Book:
- Elementary Probability for Applications
- Published online:
- 05 June 2012
- Print publication:
- 31 July 2009, pp 190-228
-
- Chapter
- Export citation
Contents
-
- Book:
- Elementary Probability for Applications
- Published online:
- 05 June 2012
- Print publication:
- 31 July 2009, pp v-vi
-
- Chapter
- Export citation
Upper bounds for a class of energies containinga non-local term
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 31 July 2009, pp. 856-886
- Print publication:
- October 2010
-
- Article
- Export citation
Evolution equations in discrete and continuous time for nonexpansive operators in Banach spaces
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 31 July 2009, pp. 809-832
- Print publication:
- October 2010
-
- Article
- Export citation
5 - Continuous Distributions
-
- Book:
- Elementary Probability for Applications
- Published online:
- 05 June 2012
- Print publication:
- 31 July 2009, pp 161-189
-
- Chapter
- Export citation
Nonlinear feedback stabilizationof a two-dimensional Burgers equation
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 31 July 2009, pp. 929-955
- Print publication:
- October 2010
-
- Article
- Export citation
4 - Markov Chains
-
- Book:
- Elementary Probability for Applications
- Published online:
- 05 June 2012
- Print publication:
- 31 July 2009, pp 114-160
-
- Chapter
- Export citation
A CLASS OF MIX DESIGN PROBLEMS: FORMULATION, SOLUTION METHODS AND APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 29 July 2009, pp. 455-474
-
- Article
-
- You have access
- Export citation
A METHOD OF IMPROVING OAR EFFICIENCY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 27 July 2009, pp. 534-540
-
- Article
-
- You have access
- Export citation
FURTHER RESULTS ON POSITIVE PERIODIC SOLUTIONS OF IMPULSIVE FUNCTIONAL DIFFERENTIAL EQUATIONS AND APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 27 July 2009, pp. 513-533
-
- Article
-
- You have access
- Export citation