Refine search
Actions for selected content:
6997 results in Mathematical modeling and methods
Eigenvalues of the Laplacian for rectilinear regions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 3 / January 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 270-281
-
- Article
-
- You have access
- Export citation
Contents of Volume 42
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 4 / April 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 581-583
-
- Article
-
- You have access
- Export citation
ANZ volume 32 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 4 / April 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Input retrieval in finite dimensional linear systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 4 / April 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 357-382
-
- Article
-
- You have access
- Export citation
ANZ volume 19 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 1 / June 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Convergence of discrete approximations for constrained minimization
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 1 / July 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 50-59
-
- Article
-
- You have access
- Export citation
Existence of solutions and optimal control problems for hyperbolic hemivariational inequalities
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 1 / July 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 51-63
-
- Article
-
- You have access
- Export citation
Convergence of degenerate-kernel methods
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 4 / December 1976
- Published online by Cambridge University Press:
- 17 February 2009, pp. 422-431
-
- Article
-
- You have access
- Export citation
On the critical conditions for an assembly of interacting thermons
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 1 / July 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 1-11
-
- Article
-
- You have access
- Export citation
Exponential decay rate of the energy of a Timoshenko beam with locally distributed feedback
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 205-220
-
- Article
-
- You have access
- Export citation
Maximum and minimum principles for capillary surface problems with prescribed contact angle
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 3 / June 1978
- Published online by Cambridge University Press:
- 17 February 2009, pp. 285-289
-
- Article
-
- You have access
- Export citation
Eigenvalues of the Laplacian for the third boundary value problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 1 / July 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 79-87
-
- Article
-
- You have access
- Export citation
Extended optima and equilibria for continuous games. I. General results
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 3 / January 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 291-307
-
- Article
-
- You have access
- Export citation
On eigensolutions of the one-speed neutron transport equation in plane geometry
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 223-230
-
- Article
-
- You have access
- Export citation
Dominated strategies in searching for evolutionary stable strategies
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 214-219
-
- Article
-
- You have access
- Export citation
Transient electromagnetic response of a layered conducting medium at asymptotically late times
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 1 / July 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 1-30
-
- Article
-
- You have access
- Export citation
Eigenvalues of the Laplacian with Neumann boundary conditions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 3 / January 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 293-309
-
- Article
-
- You have access
- Export citation
Exact solution of a difference approximation to Duffing's equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 1 / July 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 64-77
-
- Article
-
- You have access
- Export citation
Nonlinearly constrained optimal control problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 4 / April 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 517-530
-
- Article
-
- You have access
- Export citation
A comparative study of simulation techniques for two dimensional data honouring specified exponential semivariograms
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 3 / January 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 249-260
-
- Article
-
- You have access
- Export citation
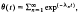 , where
, where 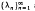 are the eigenvalues of the two-dimensional Laplacian, is studied for a variety of domains. The dependence of θ(
are the eigenvalues of the two-dimensional Laplacian, is studied for a variety of domains. The dependence of θ(