Steady plane inviscid symmetric vortex streets are flows defined in the strip R × (0, b) and periodic in x with period 2a in which the flow in (−a, a) × (0, b) is irrotational outside a vortex core on which the vorticity takes a prescribed constant value. A family of such vortex street flows, characterised by a variational principle in which the area |Aα| and the centroid yc of the vortex core Aα are fixed, will be considered. For such a family, indexed by a parameter α, suppose that the cores Aα become small in the sense that

Asymptotic estimates on functionals such as flux constant and speed are obtained.

The reduction of an important class of triple integral equations to a pair of simultaneous Fredholm equations has been carried out by Cooke [1]. In this paper, Cooke's equations are transformed to new uncoupled Fredholm equations which, for certain important cases, are shown to be simpler than Cooke's and also superior for the purposes of solution by iteration.

The problem of radially directed fluid flow through a deformable porous shell is considered. General nonlinear diffusion equations are developed for spherical, cylindrical and planar geometries. Solutions for steady flow are found in terms of an exact integral and perturbation solutions are also developed. For unsteady flow, perturbation methods are used to find approximate small-time solutions and a solution valid for slow compression rates. These solutions are used to investigate the deformation of the porous material with comparisons made between the planar and the cylindrical geometries.

John Henry Michell (1863–1940) published scientific papers only between 1890 and 1902, but included in his 23 papers from that short but productive period are some of the most important contributions ever made by an Australian mathematician. In this article I shall concentrate on the extraordinary 1898 paper “The wave resistance of a ship” Phil. Mag.(5) 45, 106–123. There are many reasons why this paper was an astounding achievement, but perhaps the most remarkable is that the resulting formula has not been improved upon to this day. In the computer age, many efforts have been made to do so, but with little success so far. The formula itself involves a triple integral of an integrand constructed from the offset data for the ship's hull, and even the task of evaluating this triple integral is not a trivial one on today's computers; another reason for admiration of Michell's own heroic hand-calculated numerical work in the 1890's. Lack of a routine algorithm for Michell's integral has inhibited its use by naval architects and ship hydrodynamic laboratories, and there has been a tendency for it to receive a bad press based on unfair comparisons, e.g. comparison of model experiments (themselves often suspect) with inaccurate computations or computations for the wrong hull, etc. The original integral is in fact quite reasonable as an engineering tool, and some new results confirming this are shown. Improvement beyond Michell is however needed in some important speed ranges, and indications are given of recent approaches that may be promising.

The Hill equation is a fundamental expression in chemical i kinetics relating velocity of response to concentration. It is known that the Hill equation is parameter identifiable in the sense that perfect data yield a unique set of defining parameters. However not all sigmoidal curves can be well fit by Hill curves. In particular the lower part of the curve can't be too shallow and the upper part can't be too steep. In this paper an exact mathematical criterion is derived to describe the degree of shallowness allowed.

In this paper, we study the global attractivity of the zero solution of a particular impulsive delay differential equation. Some sufficient conditions that guarantee every solution of the equation converges to zero are obtained.

The motion of small, near neutrally buoyant tracers in vortex flows of several types is obtained on the basis of Charwat's mathematical model, which is highly non-linear.

The solution method in the non-degenerate case expresses the squared orbital radius r2 as a product AA*, where the complex number A satisfies a second-order linear differential ‘factor equation’, generally with variable coefficients. The angular coordinate is expressed in terms of log(A*/A). Solid-type rotation and sinusoidally perturbed solid-type rotation correspond respectively to constant coefficients and sinusoidal coefficients. The former exactly yields a scalloped spiral tracer motion; the latter yields unstable tracer motion as t → ∞ except when the perturbing frequency and amplitude are rather specially related to the flow and tracer parameters. Free vortex motion is somewhat degenerate for this solution method but can be partially analyzed in terms of solutions of a generalized Emden–Fowler equation. The method can be used for other planar flow problems with a symmetry axis.

The “Hartree hybrid method” has recently been employed in one-dimensional non-linear aortic blood-flow models, and the results obtained appear to indicate that shock-waves could only form in distances which exceed physiologically meaningful values. However, when the same method is applied with greater numerical accuracy to these models, the existence of a shock-wave in the vicinity of the heart is predicted. This appears to be contrary to present belief.

We present a method for solving a class of optimal control problems involving hyperbolic partial differential equations. A numerical integration method for the solution of a general linear second-order hyperbolic partial differential equation representing the type of dynamics under consideration is given. The method, based on the piecewise bilinear finite element approximation on a rectangular mesh, is explicit. The optimal control problem is thus discretized and reduced to an ordinary optimization problem. Fast automatic differentiation is applied to calculate the exact gradient of the discretized problem so that existing optimization algorithms may be applied. Various types of constraints may be imposed on the problem. A practical application arising from the process of gas absorption is solved using the proposed method.

We examine the transmission problem in a two-dimensional domain, which consists of two different homogeneous media. We use boundary integral equation methods on the Maxwell equations governing the two media and we study the behaviour of the solution as the two different wave numbers tend to zero. We prove that as the boundary data of the general transmission problem converge uniformly to the boundary data of the corresponding electrostatic transmission problem, the general solution converges uniformly to the electrostatic one, provided we consider compact subsets of the domains.

Design of an interior point method for linear programming is discussed, and results of a simulation study reported. Emphasis is put on guessing the optimal vertex at as early a stage as possible.

In this paper we resolve the problem of controllability of nonlinear interconnected systems of neutral type. We consider two types of systems, a general one, and one in which some control appears linearly. In each case we insist that each isolated system of the interconnected problem is controlled by its own variables while taking into account the interacting effects. Controllability is proved by assuming some controllability criteria of each isolated system and some growth condition of the interconnecting function. Fixed point and open mapping theorems are used. Examples from economics and engineering are presented.

Pointwise bounds are obtained for the solution of a Dirichlet problem involving the nonlinear Liouville equation in the plane, Illustrative calculations are performed for a square domain.

An inequality involving the logarithmic mean is established. Specifically, we show that

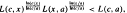
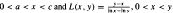where . Then several generalizations are given.