We show that Algorithm H* for the determination of the rate matrix of a block-GI/M/1 Markov chain is related by duality to Algorithm H for the determination of the fundamental matrix of a block-M/G/1 Markov chain. Duality is used to generate some efficient algorithms for finding the rate matrix in a quasi-birth-and-death process.

This paper is concerned with a generalization of the Bernstein polynomials in which the approximated function is evaluated at points spaced in geometric progression instead of the equal spacing of the original polynomials.

This paper gives a numerical method for estimating the Hausdorff-Besicovitch dimension where this differs from the fractal (or capacity or box-counting) dimension. The method has been implemented, and numerical results obtained for the set {1/n | n ∈ N} and the Cantor set. Comments about the practical use of the estimation algorithms are made.

Methods for integral equations are used to derive upper and lower pointwise bounds for the solution of a nonlinear boundary value problem arising in the steady-state finite cable model of cell membranes. Test calculations are performed to illustrate the results and the accuracy achieved is significantly better than that obtained previously by other methods.

An equation which has arisen in a study of the magentic coupling through a small rectangular aperture of dimension A × B in a thin shield wall is discussed. The magnetic polarisability of such an aperture in a conducting wall of zero thickness is known to be expressible as RHA3, in which RH is dimensionless and is a function of the aspect ratio α ≡ B/A. An asymptotic solution procedure of a certain variational formulation of this problem is described in the limiting case of large aspect ratio α. Explicit analytical formulase for the leading terms in the expansion are given. These analytical results justify the purely numerical procedures used previously to obtain approximate solutions of this formulation of the problem.

The convexity assumptions for a minimax fractional programming problem of variational type are relaxed to those of a generalised invexity situation. Sufficient optimality conditions are established under some specific assumptions. Employing the existence of a solution for the minimax variational fractional problem, three dual models, the Wolfe type dual, the Mond-Weir type dual and a one parameter dual type, are constructed. Several duality theorems concerning weak, strong and strict converse duality under the framework of invexity are proved.

We give a simple and transparent proof for the square-root method of solving the continuous-time algebraic Riccati equation. We examine some benefits of combining the square-root method with other solution methods. The iterative square-root method is also discussed. Finally, paradigm numerical examples are given to compare the square-root method with the Schur method.

In slender-body theories, one cften has to find asymptotic approximations for certain integrals, representing distribution:; of sources along a line segment. Here, such approximations are obtained by a systematic method that uses Mellin transforms. Results are given near the line (using cylindrical polar coordinates) and near the ends of the line segment (using spherical polar coordinates).

Sufficient conditions are obtained for the existence of a globally asymptotically stable strictly positive (componentwise) almost-periodic solution of a Lotka-Volterra system with almost periodic coefficients.

We use the “Brownian Bridge” of Schrödinger to model a statistical search problem in which the initial and final distributions of a random motion are given. We raise the question of how to use this information to optimally reconstruct a likely past event.

Error estimates are derived for a finite element analysis of plane steady subsonic flows described by the full potential equation. The analysis is based on the use of the theory of variational inequalities to accomodate the subsonic flow constraint and leads to a suboptimal estimate relative to that obtained for linear potential flow. We then consider an alternative dual formulation of the problem and obtain an optimal estimate subject to reasonable regularity assumptions.

The hydrodynamic pressure forces acting upon a slender fish are derived for the case of a fish swimming in a non-uniform velocity field. Possible applications are the effects on fish propulsion of swimming in waves, in turbulent eddies, and in the presence of other fish or a moving ship. The fish is assumed to be a slender body, with no vorticity shed into the fluid except at a single abrupt trailing edge located at the posterior end of the fish, and to be performing small lateral swimming undulations of its body. The non-uniform field through which the fish swims is assumed to be irrotational, and this field as well as the body undulations must be slowly-varying on the length-scale of the lateral fish dimensions. Expressions are derived for the local force and the time-averaged total thrust force. These are applied to the study of steady-state bow-riding and wave-riding of porpoises.

Pontryagin's maximum principle is derived by elementary mathematical techniques. The conditions on the functions which enter are generally somewhat more stringent than in Pontryagin's derivation, but one (practically very awkward) condition of Pontryagin can be relaxed: continuity in the time variable can be replaced by a much weaker condition.

It is shown that a problem which arose in the scheduling of two simultaneous competitions between a number of golf clubs may be reduced to that of 4- colouring the edges of a certain bipartite graph which has 4 edges meeting at each vertex. This colouring problem is solved by an analysis in terms of directed cycles, which is simple to carry through in a practical case and is easily extended to the problem with 4 replaced by 2m. The more general colouring problem with 4 replaced by any positive integer is solved by relating it to the marriage problem enunciated by Philip Hall and to the latin multiplication technique of Kaufmann but, in practical applications, this approach involves severe computational difficulties.

A delayed predator-prey system with Holling type III functional response is investigated. It is proved that the system is uniformly persistent under some appropriate conditions. By means of suitable Lyapunov functionals, sufficient conditions are derived for the local and global asymptotic stability of a positive equilibrium of the system. Numerical simulations are presented to illustrate the feasibility of our main results.

A continuous-time model of a two-sector trading economy with a finitely-saturating production function and constant population is constructed. To apply it to the farm-economy problem of optimal trading of cereal for chemical nitrogenous fertilizer and of optimal allocation of land for green manure the special assumptions are made of similar technologies in both sectors and of a nitrogen-capital loss proportional to the cereal production. Optimal-control theory is applied to get the pair of controls that maximizes an infinite-horizon integral of utility of consumption. The analysis of the model is shown to reduce to that of the Ramsey-Koopmans one-sector neoclassical model of optimal growth. Calculations of the feedback control and optimal time-paths for the standardized dimensionless model are tabulated for a range of 7 utility functions of constant elasticity of marginal utility of magnitude 1 to 4 and of production functions of degree 2 to 4. Two particular analytic solutions are given. The application of the results both to the farm-economy model and to the Ramsey-Koopmans model is illustrated.

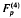Some generalisations of the Preece theorem involving the product of two Kummer's functions 1F1 are obtained using Dixon's theorem and some well-known identities. Its special cases yield various new transformations and reduction formulae involving Pathan's quadruple hypergeometric function and Srivastava's quadruple hypergeometric function F(4) and triple hypergeometric function F(3). Some known results of Preece, Pathan and Bailey are also obtained as special cases.

Competition between a finite number of searching insect parasites is modelled by differential equations and birth-death processes. In the one species case of intraspecific competition, the deterministic equilibrium is globally stable and, for large populations, approximates the mean of the stationary distribution of the process. For two species, both inter- and intraspecific competition occurs and the deterministic equilibrium is globally stable. When the birth-death process is reversible, it is shown that the mean of the stationary distribution is approximated by the equilibrium. Confluent hypergeometric functions of two variables are important to the theory.