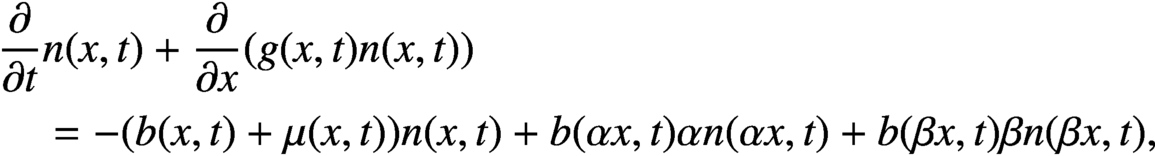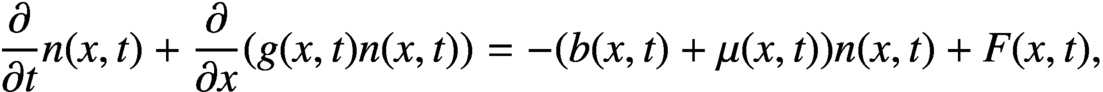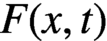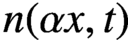Refine search
Actions for selected content:
6993 results in Mathematical modeling and methods
Dedication
-
- Book:
- Nonlinear Solid Mechanics for Finite Element Analysis: Dynamics
- Published online:
- 26 February 2021
- Print publication:
- 18 March 2021, pp v-vi
-
- Chapter
- Export citation
7 - Space and Time Discretization of Conservation Laws in Solid Dynamics
-
- Book:
- Nonlinear Solid Mechanics for Finite Element Analysis: Dynamics
- Published online:
- 26 February 2021
- Print publication:
- 18 March 2021, pp 205-245
-
- Chapter
- Export citation
ESTIMATES FOR APPROXIMATE SOLUTIONS TO A FUNCTIONAL DIFFERENTIAL EQUATION MODEL OF CELL DIVISION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 12 March 2021, pp. 469-488
-
- Article
-
- You have access
- Export citation
References
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 699-702
-
- Chapter
- Export citation
Part I - Matrix Methods
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 1-2
-
- Chapter
- Export citation
Part III - Least Squares and Optimization
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 527-528
-
- Chapter
- Export citation
5 - Analysis of Discrete Dynamical Systems
- from Part I - Matrix Methods
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 253-312
-
- Chapter
- Export citation
2 - Algebraic Eigenproblems and Their Applications
- from Part I - Matrix Methods
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 64-154
-
- Chapter
- Export citation
7 - Numerical Methods for Differential Equations
- from Part II - Numerical Methods
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 376-406
-
- Chapter
- Export citation
12 - Optimization and Root Finding of Algebraic Systems
- from Part III - Least Squares and Optimization
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 594-641
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp i-iv
-
- Chapter
- Export citation
13 - Data-Driven Methods and Reduced-Order Modeling
- from Part III - Least Squares and Optimization
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 642-698
-
- Chapter
- Export citation
Dedication
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp v-vi
-
- Chapter
- Export citation
8 - Finite-Difference Methods for Boundary-Value Problems
- from Part II - Numerical Methods
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 407-465
-
- Chapter
- Export citation
3 - Differential Eigenproblems and Their Applications
- from Part I - Matrix Methods
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 155-217
-
- Chapter
- Export citation
11 - Data Analysis: Curve Fitting and Interpolation
- from Part III - Least Squares and Optimization
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 560-593
-
- Chapter
- Export citation
6 - Computational Linear Algebra
- from Part II - Numerical Methods
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 315-375
-
- Chapter
- Export citation
9 - Finite-Difference Methods for Initial-Value Problems
- from Part II - Numerical Methods
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 466-526
-
- Chapter
- Export citation
Preface
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp xi-xvi
-
- Chapter
- Export citation
Index
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 703-710
-
- Chapter
- Export citation