Refine search
Actions for selected content:
6994 results in Mathematical modeling and methods
The Lebesgue function for generalized Hermite-Fejér interpolation on the Chebyshev nodes
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 98-109
-
- Article
-
- You have access
- Export citation
An uncoupling procedure for a class of coupled linear partial differential equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 4 / April 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 503-516
-
- Article
-
- You have access
- Export citation
Assessing regularised solutions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 1 / July 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 24-42
-
- Article
-
- You have access
- Export citation
On partly bilateral and partly unilateral generating functions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 240-245
-
- Article
-
- You have access
- Export citation
Splitting least squares and collocation procedures for two-point boundary value problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 167-193
-
- Article
-
- You have access
- Export citation
Observer-based robust H∞, control for uncertain time-delay systems
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 4 / April 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 625-634
-
- Article
-
- You have access
- Export citation
Second-order time discretization with finite-element method for partial integro-differential equations with a weakly singular kernel
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 4 / April 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 513-524
-
- Article
-
- You have access
- Export citation
On the acoustic scattering amplitude for a multi-layered Scatterer
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 4 / April 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 431-448
-
- Article
-
- You have access
- Export citation
On the constructive approximation of non-linear operators in the modelling of dynamical systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 1 / July 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 1-27
-
- Article
-
- You have access
- Export citation
Stochastic maximum principle for optimal control problem of forward and backward system
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 172-185
-
- Article
-
- You have access
- Export citation
Non-linear optimization of the material constants in Ogden's stress-deformation function for incompressinle isotropic elastic materials
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 4 / April 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 424-434
-
- Article
-
- You have access
- Export citation
Some remarks on Pauli data in quantum mechanics
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 3 / January 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 298-303
-
- Article
-
- You have access
- Export citation
On two lemmas of Brown and Shepp having application to sum sets and fractals, III
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 3 / January 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 329-337
-
- Article
-
- You have access
- Export citation
The generalized Shannon system in wavelet space
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 3 / January 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 386-400
-
- Article
-
- You have access
- Export citation
ANZ volume 21 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 1 / April 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
A reaction-diffusion model of stored bagasse
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 1 / July 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 13-34
-
- Article
-
- You have access
- Export citation
Exact solutions for redistribution by nonlinear convection-diffusion
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 3 / January 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 363-383
-
- Article
-
- You have access
- Export citation
Forced cubic Schrödinger equation with Robin boundary data: continuous dependency result
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 3 / January 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 301-311
-
- Article
-
- You have access
- Export citation
Critical point behaviour of the diffusion length for radiative transfer
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 245-257
-
- Article
-
- You have access
- Export citation
Boundary conditions for approximate differential equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 1 / July 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 54-80
-
- Article
-
- You have access
- Export citation
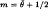 where
where 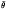 is the maximum smoothness of
is the maximum smoothness of 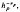 , where the critical exponent is found to be
, where the critical exponent is found to be 