Refine search
Actions for selected content:
6994 results in Mathematical modeling and methods
An investigation into the effects of heat transfer on the motion of a spherical bubble
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 3 / January 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 361-371
-
- Article
-
- You have access
- Export citation
Stability in paradigm biological systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 1 / July 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 23-34
-
- Article
-
- You have access
- Export citation
Normal shock reflection-transmission in rubber-like elastic material
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 1 / July 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 29-47
-
- Article
-
- You have access
- Export citation
A variation-of-constants formula for a linear abstract evolution equation in Hilbert space
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 4 / April 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 583-590
-
- Article
-
- You have access
- Export citation
Analytical and numerical results for flow and shock formation in two-layer gravity currents
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 1 / July 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 35-58
-
- Article
-
- You have access
- Export citation
Solution of general inhomogeneous linear difference equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 4 / April 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 466-472
-
- Article
-
- You have access
- Export citation
An integral equation for immiscible fluid isplacement in a two-dimensional porous medium or Hele-Shaw cell
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 1 / July 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 14-30
-
- Article
-
- You have access
- Export citation
Linearised evaporation about a shallow half-plane pond
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 3 / January 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 355-367
-
- Article
-
- You have access
- Export citation
What is the discrete analogue of the Painlevé property?
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 1 / July 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 21-32
-
- Article
-
- You have access
- Export citation
Examples of the nonexistence of a solution in the presence of upper and lower solutions
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 4 / April 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 591-594
-
- Article
-
- You have access
- Export citation
Reaction waves and non-constant diffusivities
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 4 / April 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 458-473
-
- Article
-
- You have access
- Export citation
Optimal Hamiltonian completions and path covers for trees, and a reduction to maximum flow
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 193-204
-
- Article
-
- You have access
- Export citation
Fractional convolution
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 257-265
-
- Article
-
- You have access
- Export citation
Numerical study of a problem in the combustion of a porous medium
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 4 / April 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 506-517
-
- Article
-
- You have access
- Export citation
A maximum principle for optimal control for a class of controlled systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 172-181
-
- Article
-
- You have access
- Export citation
ANZ volume 47 issue 3 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 3 / January 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
ANZ volume 27 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 3 / January 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Linear functionals of foliage angle density
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 4 / April 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 431-442
-
- Article
-
- You have access
- Export citation
On the scattering of waves by nearly hard or soft incomplete vertical barriers in water of infinite depth
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 3 / January 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 293-307
-
- Article
-
- You have access
- Export citation
ANZ volume 23 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 1 / July 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
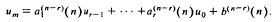
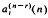 ,
, 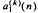 ,
, 