Refine search
Actions for selected content:
6994 results in Mathematical modeling and methods
Point-joint coordinate formulation for the dynamic analysis of generalised planar linkages
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 4 / April 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 575-589
-
- Article
-
- You have access
- Export citation
ANZ volume 38 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 1 / July 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
On two lemmas of Brown and Shepp having application to sum sets and fractals, II
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 4 / April 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 490-494
-
- Article
-
- You have access
- Export citation
Optimal control theory with general constraints
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 2 / October 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 115-126
-
- Article
-
- You have access
- Export citation
The maximum principle for a type of hereditary semilinear differential equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 194-212
-
- Article
-
- You have access
- Export citation
Solving rank one revised linear systems by the scaled ABS method
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 225-236
-
- Article
-
- You have access
- Export citation
ANZ volume 24 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 3 / January 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Numerical studies on 2-dimensional reaction-diffusion equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 223-243
-
- Article
-
- You have access
- Export citation
On the numerical solution of the diffusion equation subject to the specification of mass
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 4 / April 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 475-483
-
- Article
-
- You have access
- Export citation
The solution and the stability of a nonlinear age-structured population model
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 153-165
-
- Article
-
- You have access
- Export citation
Collocation with Chebyshev polynomials for Symm's integral equation on an interval
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 199-211
-
- Article
-
- You have access
- Export citation
Corrigendum
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 17 February 2009, p. 295
-
- Article
-
- You have access
- Export citation
Buckling analysis of plates of arbitrary shape
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 1 / July 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 77-91
-
- Article
-
- You have access
- Export citation
The construction of zonal models of dispersion in channels via matched centre manifolds
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 1 / July 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 101-125
-
- Article
-
- You have access
- Export citation
ANZ volume 23 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 2 / October 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
On neutral-delay two-species Lotka-Volterra competitive systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 3 / January 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 311-326
-
- Article
-
- You have access
- Export citation
ANZ volume 40 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f3
-
- Article
-
- You have access
- Export citation
ANZ volume 46 issue 2 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
A note on the instantaneous streamlines, pathlines and pressure contours for a cavitation bubble near a boundary
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 1 / July 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 31-44
-
- Article
-
- You have access
- Export citation
Contents of Volume 38
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 4 / April 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 590-592
-
- Article
-
- You have access
- Export citation
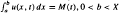 .
.