Refine search
Actions for selected content:
6994 results in Mathematical modeling and methods
Notes on a paper by J. B. Miller
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 216-220
-
- Article
-
- You have access
- Export citation
ANZ volume 27 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 1 / July 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Iterative solution of quasilinear parabolic equations by parabolic equations with constant coefficients
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 203-222
-
- Article
-
- You have access
- Export citation
Limit cycles in two spacies competition with time delays
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 2 / October 1980
- Published online by Cambridge University Press:
- 17 February 2009, pp. 148-160
-
- Article
-
- You have access
- Export citation
Diffeomorphisms on S1, projective structures and integrable systems
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 1 / July 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 169-180
-
- Article
-
- You have access
- Export citation
Phase-retardation effects at radio frequencies in flat-plate conductors
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 4 / April 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 495-510
-
- Article
-
- You have access
- Export citation
A computational method for a class of jump linear quadratic systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 4 / April 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 414-423
-
- Article
-
- You have access
- Export citation
Free-surface flow due to a source submerged in a fluid of infinite depth with two stagnant regions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 3 / January 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 368-376
-
- Article
-
- You have access
- Export citation
ANZ volume 22 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 3 / January 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
The pressure field in the gas-lubricated step slider bearing
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 3 / January 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 423-442
-
- Article
-
- You have access
- Export citation
ANZ volume 24 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 3 / January 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
A numerical scheme for the electromagnetic response in thin conductors of arbitrary planar shape
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 4 / April 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 479-497
-
- Article
-
- You have access
- Export citation
Reflection/refraction of SH-waves at a corrugated interface between two different anisotropic and vertically heterogeneous elastic solid half-spaces
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 3 / January 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 447-460
-
- Article
-
- You have access
- Export citation
A comparative study of smoothing approximations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 194-200
-
- Article
-
- You have access
- Export citation
Control of a surface of discontinuity in continuous thickness
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 3 / January 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 269-289
-
- Article
-
- You have access
- Export citation
Comparison and linearized oscillation theorems for a nonlinear partial difference equation
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 4 / April 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 552-560
-
- Article
-
- You have access
- Export citation
ANZ volume 34 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Piecewise constant collocation for first-kind boundary integral equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 3 / January 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 396-398
-
- Article
-
- You have access
- Export citation
Long wavelength vortices in time-periodic flows
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 4 / April 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 498-512
-
- Article
-
- You have access
- Export citation
A note on continuation methods for the solution of nonlinear equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. 157-164
-
- Article
-
- You have access
- Export citation

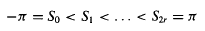

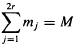 . Then γ(
. Then γ(