Refine search
Actions for selected content:
6994 results in Mathematical modeling and methods
A transformation of Cooke's treatment of some triple integral equations†
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 3 / June 1978
- Published online by Cambridge University Press:
- 17 February 2009, pp. 381-383
-
- Article
-
- You have access
- Export citation
Planform evolution in convection–an embedded centre manifold
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 174-198
-
- Article
-
- You have access
- Export citation
ANZ volume 39 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 4 / April 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Functional differential equations determining steady size distributions for populations of cells growing exponentially
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 4 / April 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 434-453
-
- Article
-
- You have access
- Export citation
ANZ volume 23 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 3 / January 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
An expansion of bivariate spline functions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 4 / April 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 527-541
-
- Article
-
- You have access
- Export citation
The problem of a rigid punch moving on a viscoelastic half-plane with inertial effects approximately included
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 2 / August 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. 198-229
-
- Article
-
- You have access
- Export citation
An exactly solvable two component classical Coulomb system
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 119-128
-
- Article
-
- You have access
- Export citation
On the stability of solutions for the p(x)-Laplacian equation and some applications to optimisation problems with state constraints
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 245-257
-
- Article
-
- You have access
- Export citation
Non-classical integrals of Bessel functions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 3 / January 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 368-378
-
- Article
-
- You have access
- Export citation
ANZ volume 48 issue 4 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 4 / April 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Fourth-order nonlinear evolution equations for surface gravity waves in the presence of a thin thermocline
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 214-229
-
- Article
-
- You have access
- Export citation
Accelerated spectral refinement Part I: simple eigenvalue
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 4 / April 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 487-507
-
- Article
-
- You have access
- Export citation
Stability of large-scale systems with lagged interconnections
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 4 / April 1980
- Published online by Cambridge University Press:
- 17 February 2009, pp. 496-509
-
- Article
-
- You have access
- Export citation
ANZ volume 48 issue 3 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 3 / January 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Extending the utility of perturbation series in problems of laminar flow in a porous pipe and a diverging channel
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 1 / July 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 118-128
-
- Article
-
- You have access
- Export citation
ANZ volume 24 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 1 / July 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Uncertainty principles invariant under the fractional Fourier transform
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 180-191
-
- Article
-
- You have access
- Export citation
Growth theorems for homogeneous second-order difference equations
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 4 / April 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 559-566
-
- Article
-
- You have access
- Export citation
Nonlinear evolution of singular disturbances to a tanh3y mixing layer
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 3 / January 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 409-427
-
- Article
-
- You have access
- Export citation
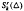 denote the vector space of functions in
denote the vector space of functions in 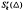 can be expressed by a series of univariate polynomials and a special bivariate finite element function in
can be expressed by a series of univariate polynomials and a special bivariate finite element function in 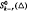 satisfying a so-called integral conformality condition system. We also give a direct sum decomposition of the space
satisfying a so-called integral conformality condition system. We also give a direct sum decomposition of the space 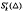 . In addition, the dimension of
. In addition, the dimension of 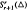 for a kind of triangulation has been determined.
for a kind of triangulation has been determined.
