Refine search
Actions for selected content:
6994 results in Mathematical modeling and methods
Criticality dependence on data and parameters for a problem in combustion theory, with temperature-dependent conductivity
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 1 / July 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 76-80
-
- Article
-
- You have access
- Export citation
Solution of a general liner difference equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 3 / January 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 314-317
-
- Article
-
- You have access
- Export citation
Saddle point and duality in the optimization theory of convex set functions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 130-137
-
- Article
-
- You have access
- Export citation
ANZ volume 43 issue 2 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Numerical integration of the axisymmetric Robinson-Trautman equation by a spectral method
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 271-280
-
- Article
-
- You have access
- Export citation
A bioeconomic model of nonselective harvesting of two competing fish species
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 299-308
-
- Article
-
- You have access
- Export citation
The iterated projection solution for the Fredholm integral equation of second kind
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 439-451
-
- Article
-
- You have access
- Export citation
Deferred correction for the integral equation eigenvalue problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 474-487
-
- Article
-
- You have access
- Export citation
ANZ volume 47 issue 3 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 3 / January 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation
On maximum principles for diffusion in the presence of three diffusion paths
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 4 / April 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 417-423
-
- Article
-
- You have access
- Export citation
Sensitivity bounds on a GI/M/n/n queueing system
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 135-149
-
- Article
-
- You have access
- Export citation
ANZ volume 31 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 4 / April 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
ANZ volume 42 issue 1 Back matter
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 17 February 2009, p. b1
-
- Article
-
- You have access
- Export citation
The Laplace transform of exp(et)
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 3 / January 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 279-287
-
- Article
-
- You have access
- Export citation
The separation of the Hamilton-Jacobi equation for the Kerr metric
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 248-259
-
- Article
-
- You have access
- Export citation
On the variational derivation of Einstein's strong field equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 3 / June 1976
- Published online by Cambridge University Press:
- 17 February 2009, pp. 381-386
-
- Article
-
- You have access
- Export citation
Pontryagin's maximum principle for optimal control of a non-well-posed parabolic differential equation involving a state constraint
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 171-184
-
- Article
-
- You have access
- Export citation
Energy intensity of inertial waves in a sphere
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 145-160
-
- Article
-
- You have access
- Export citation
Oscillatory and asymptotic behavior of solutions of nonlinear neutral-type difference equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 163-171
-
- Article
-
- You have access
- Export citation
ANZ volume 21 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 2 / August 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
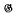 ,
, 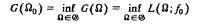
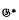 (for the definition, see the later context).
(for the definition, see the later context).