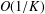Refine search
Actions for selected content:
6993 results in Mathematical modeling and methods
10 - Fourier Sampling Theory
- from Part III - Sequential Data Fundamentals
-
- Book:
- Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018, pp 322-349
-
- Chapter
- Export citation
Preface
-
- Book:
- Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018, pp xiii-xiv
-
- Chapter
- Export citation
13 - Filtering and Deconvolution
- from Part III - Sequential Data Fundamentals
-
- Book:
- Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018, pp 425-455
-
- Chapter
- Export citation
Appendix 1 - Overview of Matrix Algebra
-
- Book:
- Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018, pp 535-571
-
- Chapter
- Export citation
Appendix 2 - Uncertainty Analysis
-
- Book:
- Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018, pp 572-595
-
- Chapter
- Export citation
Dedication
-
- Book:
- Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018, pp v-vi
-
- Chapter
- Export citation
8 - Fourier Series
- from Part III - Sequential Data Fundamentals
-
- Book:
- Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018, pp 252-270
-
- Chapter
- Export citation
6 - Special Curve Fitting
- from Part II - Fitting Curves to Data
-
- Book:
- Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018, pp 178-204
-
- Chapter
- Export citation
Index
-
- Book:
- Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018, pp 599-614
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018, pp iv-iv
-
- Chapter
- Export citation
15 - Empirical Orthogonal Function (EOF) Analysis
- from Part III - Sequential Data Fundamentals
-
- Book:
- Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018, pp 495-534
-
- Chapter
- Export citation
11 - Spectral Analysis
- from Part III - Sequential Data Fundamentals
-
- Book:
- Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018, pp 350-405
-
- Chapter
- Export citation

New Handbook of Mathematical Psychology
-
- Published online:
- 13 September 2018
- Print publication:
- 27 September 2018
ANZ VOLUME 60 ISSUE 1 COVER AND BACK MATTER
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
- Published online by Cambridge University Press:
- 13 September 2018, pp. b1-b10
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 60 ISSUE 1 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
- Published online by Cambridge University Press:
- 13 September 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation

Methods of Mathematical Physics
-
- Published online:
- 12 September 2018
- Print publication:
- 18 November 1999
-
- Textbook
- Export citation
OPTION PRICING UNDER THE KOBOL MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 12 September 2018, pp. 175-190
-
- Article
-
- You have access
- Export citation

Quantitative Methods of Data Analysis for the Physical Sciences and Engineering
-
- Published online:
- 08 September 2018
- Print publication:
- 20 September 2018
EFFECT OF UNIFORM WIND FLOW ON MODULATIONAL INSTABILITY OF TWO CROSSING WAVES OVER FINITE DEPTH WATER
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
- Published online by Cambridge University Press:
- 31 August 2018, pp. 118-136
-
- Article
-
- You have access
- Export citation
ON THE
 $O(1/K)$ CONVERGENCE RATE OF THE ALTERNATING DIRECTION METHOD OF MULTIPLIERS IN A COMPLEX DOMAIN
$O(1/K)$ CONVERGENCE RATE OF THE ALTERNATING DIRECTION METHOD OF MULTIPLIERS IN A COMPLEX DOMAIN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
- Published online by Cambridge University Press:
- 30 August 2018, pp. 95-117
-
- Article
-
- You have access
- Export citation