The human retina is supplied by two vascular systems: the highly vascular choroidal, situated behind the retina; and the retinal, which is dependent on the restriction that the light path must be minimally disrupted. Between these two circulations, the avascular retinal layers depend on diffusion of metabolites through the tissue. Oxygen supply to these layers may be threatened by diseases affecting microvasculature, for example diabetes and hypertension, which may ultimately cause loss of sight.

An accurate model of retinal blood flow will therefore facilitate the study of retinal oxygen supply and, hence, the complications caused by systemic vascular disease. Here, two simple models of the blood flow and exchange of hydrogen with the retina are presented and compared qualitatively with data obtained from experimental measurements. The models capture some interesting features of the exchange and highlight effects that will need to be considered in a more sophisticated model and in the interpretation of experimental results.

We present an extension of vendor-managed inventory (VMI) problems by considering advertising and pricing policies. Unlike the results available in the literature, the demand is supposed to depend on the retail price and advertising investment policies of the manufacturer and retailers, and is a random variable. Thus, the constructed optimization model for VMI supply chain management is a stochastic bi-level programming problem, where the manufacturer is the upper level decision-maker and the retailers are the lower-level ones. By the expectation method, we first convert the stochastic model into a deterministic mathematical program with complementarity constraints (MPCC). Then, using the partially smoothing technique, the MPCC is transformed into a series of standard smooth optimization subproblems. An algorithm based on gradient information is developed to solve the original model. A sensitivity analysis has been employed to reveal the managerial implications of the constructed model and algorithm: (1) the market parameters of the model generate significant effects on the decision-making of the manufacturer and the retailers, (2) in the VMI mode, much attention should be paid to the holding and shortage costs in the decision-making.

Finding the intersection of $n$ -dimensional spheres in 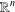$\mathbb{R}^{n}$ is an interesting problem with applications in trilateration, global positioning systems, multidimensional scaling and distance geometry. In this paper, we generalize some known results on finding the intersection of spheres, based on QR decomposition. Our main result describes the intersection of any number of $n$ -dimensional spheres without the assumption that the centres of the spheres are affinely independent. A possible application in the interval distance geometry problem is also briefly discussed.

We provide a qualitative analysis of a system of nonlinear differential equations that model the spread of alcoholism through a population. Alcoholism is viewed as an infectious disease and the model treats it within a sir framework. The model exhibits two generic types of steady-state diagram. The first of these is qualitatively the same as the steady-state diagram in the standard sir model. The second exhibits a backwards transcritical bifurcation. As a consequence of this, there is a region of bistability in which a population of problem drinkers can be sustained, even when the reproduction number is less than one. We obtain a succinct formula for this scenario when the transition between these two cases occurs.

Mealybug is an important pest of cassava plant in Thailand and tropical countries, leading to severe damage of crop yield. One of the most successful controls of mealybug spread is using its natural enemies such as green lacewings, where the development of mathematical models forecasting mealybug population dynamics improves implementation of biological control. In this work, the Sharpe–Lotka–McKendrick equation is extended and combined with an integro-differential equation to study population dynamics of mealybugs (prey) and released green lacewings (predator). Here, an age-dependent formula is employed for mealybug population. The solutions and the stability of the system are considered. The steady age distributions and their bifurcation diagrams are presented. Finally, the threshold of the rate of released green lacewings for mealybug extermination is investigated.

Semi-analytical solutions are derived for the Brusselator system in one- and two-dimensional domains. The Galerkin method is processed to approximate the governing partial differential equations via a system of ordinary differential equations. Both steady-state concentrations and transient solutions are obtained. Semi-analytical results for the stability of the model are presented for the identified critical parameter value at which a Hopf bifurcation occurs. The impact of the diffusion coefficients on the system is also considered. The results show that diffusion acts to stabilize the systems better than the equivalent nondiffusive systems with the increasing critical value of the Hopf bifurcation. Comparison between the semi-analytical and numerical solutions shows an excellent agreement with the steady-state transient solutions and the parameter values at which the Hopf bifurcations occur. Examples of stable and unstable limit cycles are given, and Hopf bifurcation points are shown to confirm the results previously calculated in the Hopf bifurcation map. The usefulness and accuracy of the semi-analytical results are confirmed by comparison with the numerical solutions of partial differential equations.

A direct search quasi-Newton algorithm is presented for local minimization of Lipschitz continuous black-box functions. The method estimates the gradient via central differences using a maximal frame around each iterate. When nonsmoothness prevents progress, a global direction search is used to locate a descent direction. Almost sure convergence to Clarke stationary point(s) is shown, where convergence is independent of the accuracy of the gradient estimates. Numerical results show that the method is effective in practice.

A numerical comparison of the Monte Carlo (MC) simulation and the finite-difference method for pricing European options under a regime-switching framework is presented in this paper. We consider pricing options on stocks having two to four volatility regimes. Numerical results show that the MC simulation outperforms the Crank–Nicolson (CN) finite-difference method in both the low-frequency case and the high-frequency case. Even though both methods have linear growth, as the number of regimes increases, the computational time of CN grows much faster than that of MC. In addition, for the two-state case, we propose a much faster simulation algorithm whose computational time is almost independent of the switching frequency. We also investigate the performances of two variance-reduction techniques: antithetic variates and control variates, to further improve the efficiency of the simulation.

We prove that the probability substitution matrices obtained from a continuous-time Markov chain form a multiplicatively closed set if and only if the rate matrices associated with the chain form a linear space spanning a Lie algebra. The key original contribution we make is to overcome an obstruction, due to the presence of inequalities that are unavoidable in the probabilistic application, which prevents free manipulation of terms in the Baker–Campbell–Haursdorff formula.

A new minimization principle for the Poisson equation using two variables – the solution and the gradient of the solution – is introduced. This principle allows us to use any conforming finite element spaces for both variables, where the finite element spaces do not need to satisfy the so-called inf–sup condition. A numerical example demonstrates the superiority of this approach.

We study bound states in weakly deformed and heterogeneous waveguides, and compare analytical predictions using a recently developed perturbative method with precise numerical results for three different configurations: a homogeneous asymmetric waveguide, a heterogenous asymmetric waveguide and a homogeneous broken strip. We have found excellent agreement between the analytical and numerical results in all the examples; this provides a numerical verification of the analytical approach.