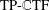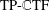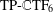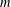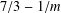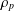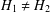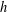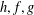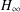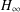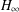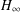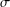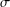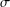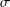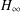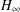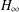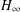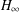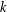Refine search
Actions for selected content:
6993 results in Mathematical modeling and methods
EDITORIAL: MATHEMATICAL METHODS FOR APPLICATIONS
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 19 June 2017, pp. 209-210
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 58 ISSUE 3-4 COVER AND BACK MATTER
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 19 June 2017, pp. b1-b15
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 58 ISSUE 3-4 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 19 June 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
IMAGE INPAINTING FROM PARTIAL NOISY DATA BY DIRECTIONAL COMPLEX TIGHT FRAMELETS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 26 May 2017, pp. 247-255
-
- Article
-
- You have access
- Export citation
SCHEDULING ON TWO PARALLEL MACHINES WITH TWO DEDICATED SERVERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 25 May 2017, pp. 314-323
-
- Article
-
- You have access
- Export citation
PARALLEL MACHINE SCHEDULING WITH JOB DELIVERY COORDINATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 25 May 2017, pp. 306-313
-
- Article
-
- You have access
- Export citation
COVERAGE PERFORMANCE OF COGNITIVE RADIO NETWORKS POWERED BY RENEWABLE ENERGY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 24 May 2017, pp. 287-305
-
- Article
-
- You have access
- Export citation
ON MULTI-ASSET SPREAD OPTION PRICING IN A WICK–ITÔ–SKOROHOD INTEGRAL FRAMEWORK
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 24 May 2017, pp. 386-396
-
- Article
-
- You have access
- Export citation
NEW GENERALIZED
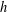 $h$ -IMPLICATIONS
$h$ -IMPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 24 May 2017, pp. 276-286
-
- Article
-
- You have access
- Export citation
PRICING PERPETUAL TIMER OPTION UNDER THE STOCHASTIC VOLATILITY MODEL OF HULL–WHITE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 16 May 2017, pp. 406-416
-
- Article
-
- You have access
- Export citation
DELAYED FUZZY
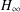 $H_{\infty }$ CONTROL OF OFFSHORE STEEL JACKET PLATFORMS
$H_{\infty }$ CONTROL OF OFFSHORE STEEL JACKET PLATFORMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 16 May 2017, pp. 446-454
-
- Article
-
- You have access
- Export citation
APPROXIMATE CONTROLLABILITY OF POPULATION DYNAMICS WITH SIZE DEPENDENCE AND SPATIAL DISTRIBUTION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 16 May 2017, pp. 474-481
-
- Article
-
- You have access
- Export citation
A NOTE ON MARKOVIAN QUANTUM DYNAMICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 436-445
-
- Article
-
- You have access
- Export citation
COMPETITIVE ANALYSIS OF INTERRELATED PRICE ONLINE INVENTORY PROBLEMS WITH DEMANDS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 368-378
-
- Article
-
- You have access
- Export citation
CHARACTERIZATIONS OF THE BOREL
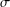 $\unicode[STIX]{x1D70E}$ -FIELDS OF THE FUZZY NUMBER SPACE
$\unicode[STIX]{x1D70E}$ -FIELDS OF THE FUZZY NUMBER SPACE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 265-275
-
- Article
-
- You have access
- Export citation
DELAYED STATE FEEDBACK
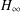 $H_{\infty }$ CONTROL FOR PERIODIC-REVIEW INVENTORY SYSTEMS
$H_{\infty }$ CONTROL FOR PERIODIC-REVIEW INVENTORY SYSTEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 397-405
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC BEHAVIOUR OF A CLASS OF RESOURCE COMPETITION BIOLOGY SPECIES SYSTEM BY THE FRACTIONAL BROWNIAN MOTION
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 491-499
-
- Article
-
- You have access
- Export citation
APPROXIMATION BY SPHERICAL NEURAL NETWORKS WITH ZONAL FUNCTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 238-246
-
- Article
-
- You have access
- Export citation
NETWORK DESIGN FOR MINIMUM SPANNING TREES UNDER HAMMING DISTANCE
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 342-349
-
- Article
-
- You have access
- Export citation
COMPLEX DEMODULATION: A NOVEL TIME SERIES METHOD FOR ANALYSING SEASONAL INFECTIOUS DISEASES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 1 / July 2017
- Published online by Cambridge University Press:
- 21 April 2017, pp. 51-60
-
- Article
-
- You have access
- Export citation