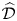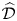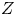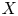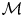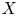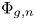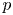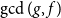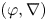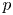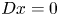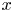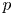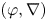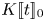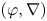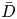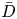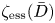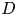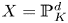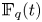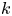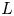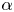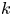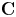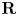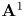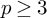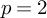Refine listing
Actions for selected content:
361 results in 14Gxx
Corrections to “Value sets of sparse polynomials”
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 1071-1073
- Print publication:
- December 2022
-
- Article
- Export citation
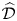 $\widehat {\mathcal {D}}$-modules on rigid analytic spaces III: weak holonomicity and operations
$\widehat {\mathcal {D}}$-modules on rigid analytic spaces III: weak holonomicity and operations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 28 October 2021, pp. 2553-2584
- Print publication:
- December 2021
-
- Article
- Export citation
The essential dimension of congruence covers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 27 October 2021, pp. 2407-2432
- Print publication:
- November 2021
-
- Article
- Export citation
AUTOMORPHIC LEFSCHETZ PROPERTIES FOR NONCOMPACT ARITHMETIC MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1655-1702
- Print publication:
- July 2023
-
- Article
- Export citation
Period sheaves via derived de Rham cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2021, pp. 2377-2406
- Print publication:
- November 2021
-
- Article
- Export citation
LOGARITHMIC DE RHAM–WITT COMPLEXES VIA THE DÉCALAGE OPERATOR
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 26 August 2021, pp. 1319-1382
- Print publication:
- May 2023
-
- Article
- Export citation
Positivity of Hodge bundles of abelian varieties over some function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 03 August 2021, pp. 1964-2000
- Print publication:
- September 2021
-
- Article
- Export citation
Average-case complexity of the Euclidean algorithm with a fixed polynomial over a finite field
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 166-183
-
- Article
- Export citation
GEOMETRIC QUADRATIC CHABAUTY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 17 June 2021, pp. 279-333
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
Logarithmic growth filtrations for
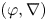 $(\varphi ,\nabla )$-modules over the bounded Robba ring
$(\varphi ,\nabla )$-modules over the bounded Robba ring
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 1265-1301
- Print publication:
- June 2021
-
- Article
- Export citation
Successive minima and asymptotic slopes in Arakelov geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1302-1339
- Print publication:
- June 2021
-
- Article
- Export citation
Automorphic vector bundles on the stack of G-zips
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 03 May 2021, e37
-
- Article
-
- You have access
- Open access
- Export citation
Rational points and derived equivalence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 1036-1050
- Print publication:
- May 2021
-
- Article
- Export citation
Explicit methods for the Hasse norm principle and applications to An and Sn extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 489-529
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
CM liftings of
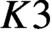 $K3$ surfaces over finite fields and their applications to the Tate conjecture
$K3$ surfaces over finite fields and their applications to the Tate conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 April 2021, e29
-
- Article
-
- You have access
- Open access
- Export citation
An arithmetic count of the lines on a smooth cubic surface
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 08 April 2021, pp. 677-709
- Print publication:
- April 2021
-
- Article
- Export citation
UNIRATIONALITY AND GEOMETRIC UNIRATIONALITY FOR HYPERSURFACES IN POSITIVE CHARACTERISTICS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 08 March 2021, pp. 1831-1847
- Print publication:
- September 2022
-
- Article
- Export citation
Zariski dense orbits for regular self-maps on split semiabelian varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 05 March 2021, pp. 116-122
- Print publication:
- March 2022
-
- Article
- Export citation
Some effectivity questions for plane Cremona transformations in the context of symmetric key cryptography
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 01 March 2021, pp. 1-28
-
- Article
- Export citation
Rigid-analytic varieties with projective reduction violating Hodge symmetry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 625-640
- Print publication:
- March 2021
-
- Article
- Export citation