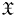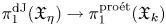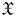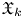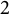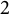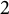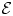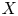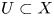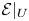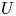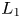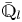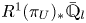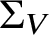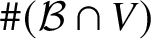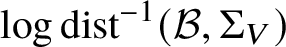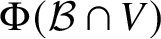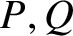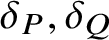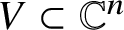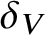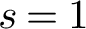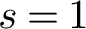Refine listing
Actions for selected content:
361 results in 14Gxx
The six-functor formalism for rigid analytic motives
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 08 August 2022, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Specialization for the pro-étale fundamental group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 27 September 2022, pp. 1713-1745
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion codimension
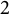 $2$ cycles on supersingular abelian varieties
$2$ cycles on supersingular abelian varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 458-466
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some cases of Kudla’s modularity conjecture for unitary Shimura varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Curves of maximal moduli on K3 surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 08 June 2022, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric consistency of Manin's conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 August 2022, pp. 1375-1427
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tropical moments of tropical Jacobians
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 May 2022, pp. 1045-1075
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion points on isogenous abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 20 July 2022, pp. 1020-1051
- Print publication:
- May 2022
-
- Article
- Export citation
Perfect points on curves of genus 1 and consequences for supersingular K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 22 July 2022, pp. 1052-1083
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regular integral models for Shimura varieties of orthogonal type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 831-867
- Print publication:
- April 2022
-
- Article
- Export citation
Reductions of abelian surfaces over global function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 16 June 2022, pp. 893-950
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rank 2 local systems and abelian varieties II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 868-892
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Kawamata–Viehweg vanishing theorem for log del Pezzo surfaces in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 750-763
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Point counting for foliations over number fields
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 March 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
VALUES OF ZETA FUNCTIONS OF ARITHMETIC SURFACES AT
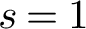 $s=1$
$s=1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 28 February 2022, pp. 2455-2496
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE GEOMETRY OF THE PAPPAS–RAPOPORT MODELS FOR PEL SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 18 February 2022, pp. 2403-2445
- Print publication:
- September 2023
-
- Article
- Export citation
The six functors for Zariski-constructible sheaves in rigid geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 26 April 2022, pp. 437-482
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Faltings height and Néron–Tate height of a theta divisor
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 1-32
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum: Generic rank of Betti map and unlikely intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 05 January 2022, pp. 2747-2748
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
GEOMETRIC WEIGHT-SHIFTING OPERATORS ON HILBERT MODULAR FORMS IN CHARACTERISTIC p
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 1871-1930
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation