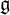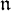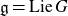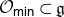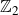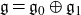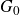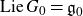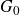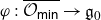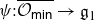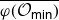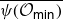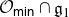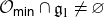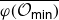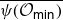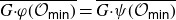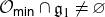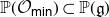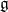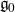Refine listing
Actions for selected content:
145 results in 14Lxx
Kappa classes on KSBA spaces
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformation theory for prismatic G-displays
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 21 March 2025, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prismatic Dieudonné Theory – ERRATUM
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generic stabilizers for simple algebraic groups acting on orthogonal and symplectic Grassmannians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chai's conjecture for semiabelian Jacobians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 120-147
- Print publication:
- January 2025
-
- Article
- Export citation
FINITE-DIMENSIONAL DIFFERENTIAL-ALGEBRAIC PERMUTATION GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 603-626
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A McKay Correspondence in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lifting G-Valued Galois Representations when
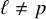 $\ell \neq p$
$\ell \neq p$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Height functions on Hecke orbits and the generalised André–Pink–Zannier conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2531-2584
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENDING TORSORS UNDER QUASI-FINITE FLAT GROUP SCHEMES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 45-54
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On irreducible representations of Fuchsian groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 27 August 2024, pp. 970-990
- Print publication:
- December 2024
-
- Article
- Export citation
Affine Bruhat order and Demazure products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 April 2024, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the moduli of hypersurfaces in toric orbifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 14 March 2024, pp. 577-616
-
- Article
- Export citation
Lie algebra actions on module categories for truncated shifted yangians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 31 January 2024, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Bezrukavnikov–Kaledin quantization of symplectic varieties in characteristic p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 411-450
- Print publication:
- February 2024
-
- Article
- Export citation
The Grothendieck–Serre conjecture over valuation rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 317-355
- Print publication:
- February 2024
-
- Article
- Export citation
Stability conditions for polarised varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 20 November 2023, e104
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Frobenius semiradical, generic stabilizers, and Poisson center for nilradicals
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 2019-2048
- Print publication:
- December 2024
-
- Article
- Export citation
NON-ISOMORPHIC SMOOTH COMPACTIFICATIONS OF THE MODULI SPACE OF CUBIC SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 03 October 2023, pp. 315-365
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Projections of the minimal nilpotent orbit in a simple Lie algebra and secant varieties
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 13 July 2023, pp. 595-624
- Print publication:
- November 2023
-
- Article
- Export citation
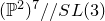
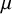
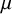
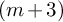
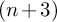
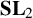
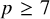
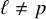
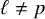
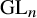
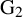
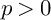
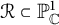
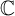
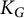
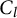
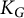
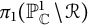
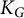
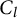
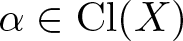



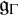


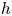
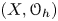
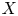
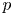
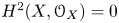
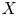
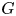
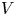
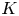
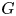
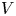
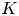
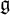
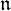
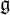
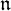
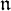
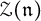 of the symmetric algebra
of the symmetric algebra 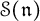 ,
, 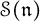 as
as 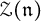 -module, and
-module, and