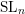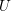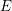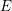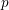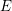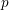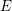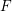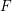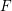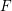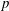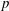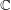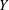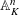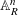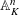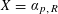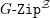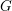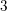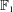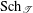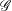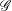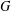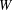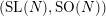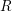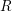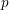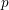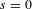Refine listing
Actions for selected content:
145 results in 14Lxx
ON TORUS ACTIONS OF HIGHER COMPLEXITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 31 October 2019, e38
-
- Article
-
- You have access
- Open access
- Export citation
Le principe de Hasse pour les espaces homogènes : réduction au cas des stabilisateurs finis
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 1568-1593
- Print publication:
- August 2019
-
- Article
- Export citation
Families of Picard modular forms and an application to the Bloch–Kato conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 1327-1401
- Print publication:
- July 2019
-
- Article
- Export citation
Ascending chain condition for
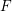 $F$-pure thresholds on a fixed strongly
$F$-pure thresholds on a fixed strongly 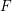 $F$-regular germ
$F$-regular germ
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 28 May 2019, pp. 1194-1223
- Print publication:
- June 2019
-
- Article
- Export citation
Local Shtukas and Divisible Local Anderson Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1163-1207
- Print publication:
- October 2019
-
- Article
-
- You have access
- Open access
- Export citation
Tits Buildings and K-Stability
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 799-815
-
- Article
- Export citation
Fixed point theorems involving numerical invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 260-288
- Print publication:
- February 2019
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Degenerations of Leibniz and Anticommutative Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 539-549
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
On Deformations of 1-motives
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 11-22
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
MODELS OF TORSORS OVER AFFINE SPACES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 530-541
- Print publication:
- 2019
-
- Article
- Export citation
Commuting Varieties for Nilpotent Radicals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 559-594
-
- Article
- Export citation
Automorphic vector bundles with global sections on
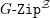 $G\text{-}\mathtt{Zip}^{{\mathcal{Z}}}$-schemes
$G\text{-}\mathtt{Zip}^{{\mathcal{Z}}}$-schemes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 31 October 2018, pp. 2586-2605
- Print publication:
- December 2018
-
- Article
- Export citation
THE GEOMETRY OF BLUEPRINTS PART II: TITS–WEYL MODELS OF ALGEBRAIC GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 23 October 2018, e20
-
- Article
-
- You have access
- Open access
- Export citation
The Variety of Two-dimensional Algebras Over an Algebraically Closed Field
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 16 October 2018, pp. 819-842
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Springer correspondence for the split symmetric pair in type
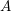 $A$
$A$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 11 October 2018, pp. 2403-2425
- Print publication:
- November 2018
-
- Article
- Export citation
Dieudonné theory over semiperfect rings and perfectoid rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 17 August 2018, pp. 1974-2004
- Print publication:
- September 2018
-
- Article
- Export citation
On a purely inseparable analogue ofthe Abhyankar conjecture for affine curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 1633-1658
- Print publication:
- August 2018
-
- Article
- Export citation
RAPOPORT–ZINK SPACES OF HODGE TYPE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 07 June 2018, e8
-
- Article
-
- You have access
- Open access
- Export citation
The volume of singular Kähler–Einstein Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 1131-1158
- Print publication:
- June 2018
-
- Article
- Export citation
PERIODS OF DRINFELD MODULES AND LOCAL SHTUKAS WITH COMPLEX MULTIPLICATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 20 March 2018, pp. 175-208
- Print publication:
- January 2020
-
- Article
- Export citation