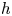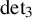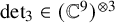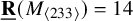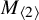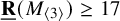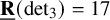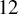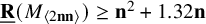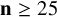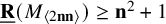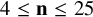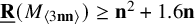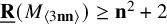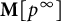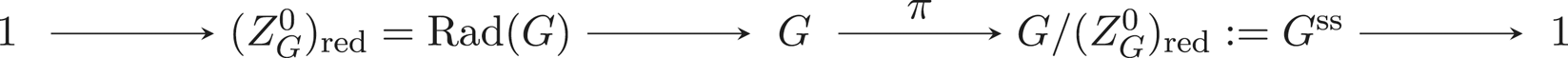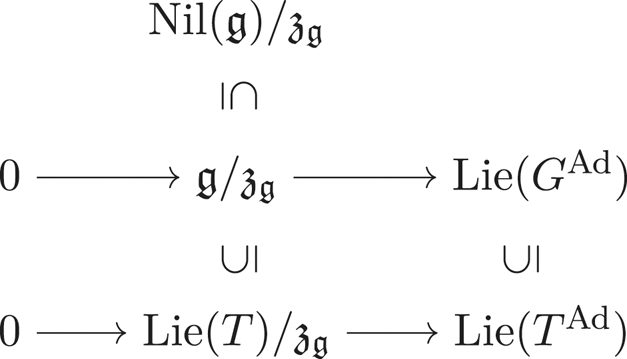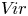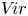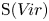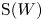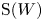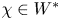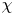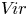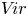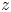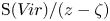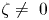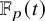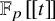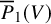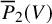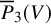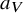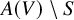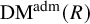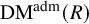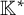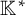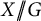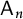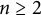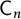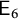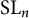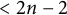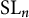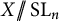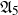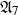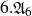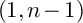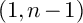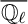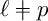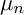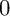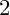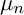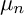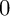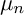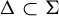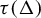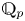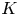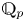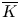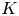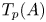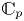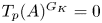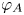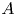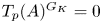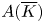Refine listing
Actions for selected content:
145 results in 14Lxx
Generic differential equations are strongly minimal
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 08 June 2023, pp. 1387-1412
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New lower bounds for matrix multiplication and
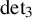 $\operatorname {det}_3$
$\operatorname {det}_3$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 29 May 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Log p-divisible groups associated with log 1-motives
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 28 April 2023, pp. 946-983
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integration questions in separably good characteristics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 890-932
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Poisson spectrum of the symmetric algebra of the Virasoro algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 18 April 2023, pp. 933-984
- Print publication:
- May 2023
-
- Article
- Export citation
Grassmanniennes affines tordues sur les entiers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 February 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective characterization of quasi-abelian surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 February 2023, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prismatic Dieudonné Theory
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 January 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small G-varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 04 January 2023, pp. 173-215
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite quasisimple groups acting on rationally connected threefolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 06 December 2022, pp. 531-568
- Print publication:
- May 2023
-
- Article
- Export citation
COHOMOLOGY OF THE BRUHAT–TITS STRATA IN THE UNRAMIFIED UNITARY RAPOPORT–ZINK SPACE OF SIGNATURE
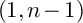 $(1,n-1)$
$(1,n-1)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 470-497
- Print publication:
- June 2023
-
- Article
- Export citation
On canonical Fano intrinsic quadrics
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 07 November 2022, pp. 288-309
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TORSORS AND STABLE EQUIVARIANT BIRATIONAL GEOMETRY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 11 October 2022, pp. 275-297
- Print publication:
- June 2023
-
- Article
- Export citation
CHARACTER STACKS ARE PORC COUNT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 289-310
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON
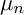 $\mu _{n}$-ACTIONS ON K3 SURFACES IN POSITIVE CHARACTERISTIC
$\mu _{n}$-ACTIONS ON K3 SURFACES IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 11-49
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On images of subshifts under embeddings of symbolic varieties
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 3131-3149
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximum likelihood estimation for tensor normal models via castling transforms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 01 July 2022, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On p-adic uniformization of abelian varieties with good reduction
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1449-1476
- Print publication:
- July 2022
-
- Article
- Export citation
Grothendieck–Serre in the quasi-split unramified case
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 29 March 2022, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL THEORY OF FIELDS WITH FINITE GROUP SCHEME ACTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 14 March 2022, pp. 1443-1468
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation