Refine listing
Actions for selected content:
194 results in 14Mxx
Produit eulérien motivique et courbes rationnelles sur les variétés toriques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1360-1400
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
Euler characteristic of primitive T-hypersurfaces and maximal surfaces
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 23 July 2009, pp. 1-27
- Print publication:
- January 2010
-
- Article
- Export citation
Parabolic category O, perverse sheaves on Grassmannians, Springer fibres and Khovanov homology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 954-992
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
The category of toric stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 718-746
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Local models in the ramified case. III Unitary groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 26 March 2009, pp. 507-564
- Print publication:
- July 2009
-
- Article
- Export citation
The Minimal Resolution Conjecture for Points on the Cubic Surface
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 29-49
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
Moduli of toric vector bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1199-1213
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Varieties with quadratic entry locus, II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 949-962
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
On the unramified spectrum of spherical varieties over p-adic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 978-1016
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
A generalized Gaeta’s theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 689-704
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Quantum cohomology of the Grassmannian and alternate Thom–Sebastiani
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 221-246
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
C2 building and projective space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 383-402
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
On the Gauss maps of singular projective varieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 119-130
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
On the action of the unitary group on the projective plane over a local field
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 371-397
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
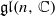 we prove that the centre of the principal block 𝒪
we prove that the centre of the principal block 𝒪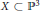
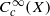 are in natural ‘almost bijection’ with a number of copies of
are in natural ‘almost bijection’ with a number of copies of 