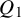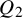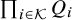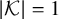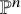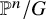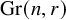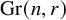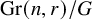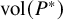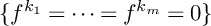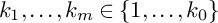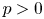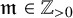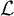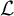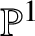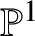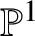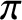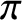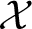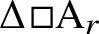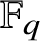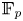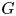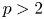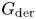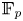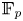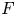Refine listing
Actions for selected content:
199 results in 14Mxx
A generalized Sylvester–Gallai-type theorem for quadratic polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 December 2022, e112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unwinding Toric Degenerations and Mirror Symmetry for Grassmannians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 14 December 2022, e111
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the maximum dual volume of a canonical Fano polytope
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 December 2022, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE MILNOR FIBRATION OF CERTAIN NEWTON DEGENERATE FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 410-433
-
- Article
- Export citation
Higher index Fano varieties with finitely many birational automorphisms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 02 December 2022, pp. 2033-2045
- Print publication:
- November 2022
-
- Article
- Export citation
Open-closed Gromov-Witten invariants of 3-dimensional Calabi-Yau smooth toric DM stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 July 2022, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Calabi–Yau properties of Postnikov diagrams
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 July 2022, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NORMALISED TANGENT BUNDLE, VARIETIES WITH SMALL CODEGREE AND PSEUDOEFFECTIVE THRESHOLD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 15 July 2022, pp. 149-206
- Print publication:
- January 2024
-
- Article
- Export citation
On the topological complexity and zero-divisor cup-length of real Grassmannians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 31 March 2022, pp. 702-717
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Grothendieck–Serre in the quasi-split unramified case
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 29 March 2022, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unramified logarithmic Hodge–Witt cohomology and
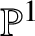 $\mathbb {P}^1$-invariance
$\mathbb {P}^1$-invariance
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 March 2022, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stringy invariants and toric Artin stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 07 February 2022, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On combinatorics of the Arthur trace formula, convex polytopes, and toric varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 27 January 2022, pp. 375-420
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the multiplication of spherical functions of reductive spherical pairs of type A
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 09 December 2021, pp. 341-374
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TRUNCATED AFFINE SPRINGER FIBERS AND ARTHUR’S WEIGHTED ORBITAL INTEGRALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. 1757-1818
- Print publication:
- July 2023
-
- Article
- Export citation
Geometric vertex decomposition and liaison
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 19 October 2021, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wall-crossings and a categorification of K-theory stable bases of the Springer resolution
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2021, pp. 2341-2376
- Print publication:
- November 2021
-
- Article
- Export citation
Cluster Structures on Double Bott–Samelson Cells
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 29 September 2021, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Central elements in affine mod p Hecke algebras via perverse
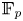 $\mathbb {F}_p$-sheaves
$\mathbb {F}_p$-sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 14 September 2021, pp. 2215-2241
- Print publication:
- October 2021
-
- Article
- Export citation
Fano-type surfaces with large cyclic automorphisms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 05 August 2021, e54
-
- Article
-
- You have access
- Open access
- Export citation