We give a simple proof of the Lalonde–McDuff Conjecture for aspherical manifolds.

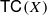The topological complexity is a numerical homotopy invariant of a topological space 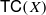X which is motivated by robotics and is similar in spirit to the classical Lusternik–Schnirelmann category of X. Given a mechanical system with configuration space X, the invariant measures the complexity of motion planning algorithms which can be designed for the system. In this paper, we compute the topological complexity of the configuration space of n distinct ordered points on an orientable surface, for both closed and punctured surfaces. Our main tool is a theorem of B. Totaro describing the cohomology of configuration spaces of algebraic varieties. For configuration spaces of punctured surfaces, this is used in conjunction with techniques from the theory of mixed Hodge structures.

The main result indicates that every finitely generated, residually finite, torsion-free, cohopfian group having on free Abelian subgroup of rank two is hyperhopfian. The argument relies on earlier work and ideas of Hirshon. As a corollary, fundamental groups of all closed hyperbolic manifolds are hyperhopfian.

Using various facts about principal bundles over a space, we give a unified treatment of several theorems about the structure of stable separable continuous-trace algebras, their automorphisms, and their K-theory. We also present a classification of real continuous-trace algebras from the same point of view.

Topological algebra bundles whose fibre (-algebras) admit functional representations constitute a category, antiequivalent with that of (topological) fibre bundles having completely regular bundle spaces and locally compact fibres.

We have defined and studied some pseudogroups of local diffeomorphisms which generalise the complex analytic pseudogroups. A 4-dimensional (or 8-dimensional) manifold modelled on these ‘Further pseudogroups’ turns out to be a quaternionic (respectively octonionic) manifold.

We characterise compact Further manifolds as being products of compact Riemann surfaces with appropriate dimensional spheres. It then transpires that a connected compact quaternionic (H) (respectively O) manifold X, minus a finite number of circles (its ‘real set’), is the orientation double covering of the product Y × P2, (respectively Y×P6), where Y is a connected surface equipped with a canonical conformal structure and Pn is n-dimensonal real projective space.

A corollary is that the only simply-connected compact manifolds which can allow H (respectively O) structure are S4 and S2 × S2 (respectively S8 and S2×S6).

Previous authors, for example Marchiafava and Salamon, have studied very closely-related classes of manifolds by differential geometric methods. Our techniques in this paper are function theoretic and topological.

By a theorem of Fell and Tomiyama-Takesaki, an N-homogeneous C*-algebra with spectrum X has the form Γ(E) for some bundle E over X with fibre MN(C), and its isomorphism class is determined by that of E and its pull-backs f*E along homeomorphisms f of X. We describe the homogeneous C*-algebras with spectrum T2 or T3 by classifying the MN-bundles over Tk using elementary homotopy theory. We then use our results to determine the isomorphism classes of a variety of transformation group C*-algebras, twisted group C*-algebras and more general crossed products.

This paper concerns conditions under which the classifying space functor transforms a fibre square of topological monoids into a fibre square of spaces. Before stating our results precisely, we first develop some relevant points concerning the continuity of functors.