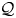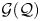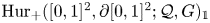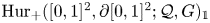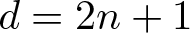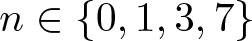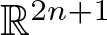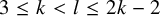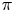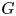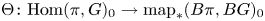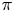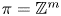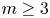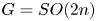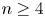Refine listing
Actions for selected content:
90 results in 55Rxx
Characteristic numbers of manifold bundles over spheres and positive curvature via block bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 August 2025, e138
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mapping class groups of h-cobordant manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 August 2025, e132
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the finiteness of the classifying space of diffeomorphisms of reducible three manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 April 2025, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exotic Fusion Systems Related to Sporadic Simple Groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 331-384
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SU(2)-bundles over highly connected 8-manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 February 2025, pp. 1-30
-
- Article
- Export citation
Graphing, homotopy groups of spheres, and spaces of long links and knots
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FORBIDDEN PARTITION CONFIGURATION SPACES OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 12 February 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free torus actions and twisted suspensions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant parametrized topological complexity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-24
-
- Article
- Export citation
PL homeomorphisms of surfaces and codimension 2 PL foliations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2684-2703
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomological and motivic inclusion–exclusion
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 2228-2283
- Print publication:
- September 2024
-
- Article
- Export citation
Deloopings of Hurwitz spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1651-1714
- Print publication:
- July 2024
-
- Article
- Export citation
Torsion in classifying spaces of gauge groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global index of real polynomials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 March 2024, pp. 1-29
-
- Article
- Export citation
Unit sphere fibrations in Euclidean space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 287-298
-
- Article
- Export citation
PERFECTING GROUP SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 2549-2591
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classifying spaces for families of abelian subgroups of braid groups, RAAGs and graphs of abelian groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 290-307
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The stable cohomology of self-equivalences of connected sums of products of spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The space of commuting elements in a Lie group and maps between classifying spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 27 October 2023, pp. 735-755
- Print publication:
- June 2025
-
- Article
- Export citation
CONDITIONAL FLATNESS, FIBERWISE LOCALIZATIONS, AND ADMISSIBLE REFLECTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 200-220
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation