Refine listing
Actions for selected content:
90 results in 55Rxx
Cohomology of Flat Principal Bundles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 22 May 2018, pp. 869-877
-
- Article
- Export citation
A Remark on Configuration Spaces of Two Points
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 11 April 2018, pp. 599-605
-
- Article
- Export citation
Rational Cup Product and Algebraic K0-Groups of Rings of Continuous Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 10 April 2018, pp. 607-622
-
- Article
- Export citation
ON THE SYMMETRIC SQUARES OF COMPLEX AND QUATERNIONIC PROJECTIVE SPACE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 13 February 2018, pp. 703-729
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
THE COHOMOLOGY RING OF ORBIT SPACES OF FREE
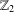 $\mathbb{Z}_{2}$ -ACTIONS ON SOME DOLD MANIFOLDS
$\mathbb{Z}_{2}$ -ACTIONS ON SOME DOLD MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 02 February 2018, pp. 340-348
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
DISMANTLABLE CLASSIFYING SPACE FOR THE FAMILY OF PARABOLIC SUBGROUPS OF A RELATIVELY HYPERBOLIC GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 11 April 2017, pp. 329-345
- Print publication:
- March 2019
-
- Article
- Export citation
Brown–Peterson cohomology from Morava
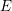 $E$ -theory
$E$ -theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 780-819
- Print publication:
- April 2017
-
- Article
- Export citation
Tautological rings for high-dimensional manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 851-866
- Print publication:
- April 2017
-
- Article
- Export citation
Tautological rings of spaces of pointed genus two curves of compact type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 17 June 2016, pp. 1398-1420
- Print publication:
- July 2016
-
- Article
- Export citation
Equivariant Maps from Stiefel Bundles to Vector Bundles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 01 June 2016, pp. 231-250
-
- Article
- Export citation
THE INTEGRAL COHOMOLOGY OF THE HILBERT SCHEME OF TWO POINTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 27 April 2016, e8
-
- Article
-
- You have access
- Open access
- Export citation
THE GROMOV-LAWSON-ROSENBERG CONJECTURE FOR THE SEMI-DIHEDRAL GROUP OF ORDER 16
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 365-386
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
Co-H-Spaces and Almost Localization
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 323-332
-
- Article
-
- You have access
- Export citation
On derivations and elementary operators on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 21 March 2013, pp. 515-534
-
- Article
-
- You have access
- Export citation
Spaces with Noetherian cohomology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 13-25
-
- Article
-
- You have access
- Export citation
S3-free 2-fusion systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 27-48
-
- Article
-
- You have access
- Export citation
Nilpotence in group cohomology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 151-175
-
- Article
-
- You have access
- Export citation
Commuting elements in central products of special unitary groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 24 October 2012, pp. 1-12
-
- Article
-
- You have access
- Export citation
Cohomological uniqueness of some p-groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 August 2012, pp. 449-468
-
- Article
-
- You have access
- Export citation
TELESCOPIC LINKAGES AND A TOPOLOGICAL APPROACH TO PHASE TRANSITIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 03 June 2011, pp. 183-195
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
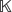
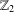
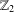
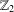
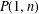

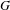
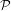
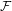
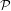
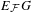
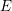
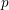
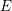
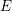
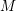
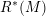
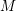
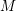
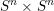



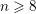
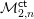
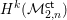
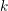

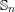

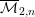
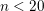
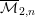
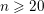
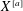
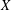

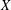
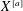
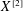
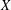
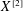
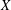
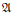 over the maximal ideal space of the centre of
over the maximal ideal space of the centre of 