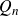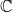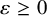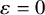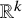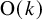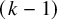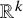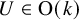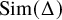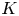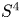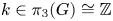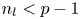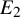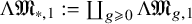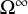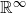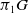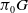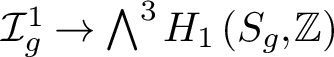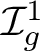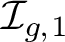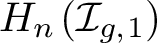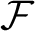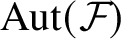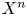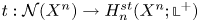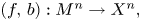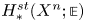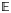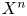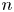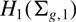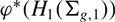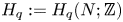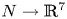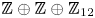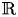Refine listing
Actions for selected content:
90 results in 55Rxx
Coniveau filtrations and Milnor operation
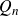 $Q_n$
$Q_n$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 08 May 2023, pp. 521-538
- Print publication:
- November 2023
-
- Article
- Export citation
Approximate and discrete Euclidean vector bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 21 March 2023, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Families of similar simplices inscribed in most smoothly embedded spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 November 2022, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enough vector bundles on orbispaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 28 November 2022, pp. 2046-2081
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The mod-p homology of the classifying spaces of certain gauge groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 1805-1817
- Print publication:
- December 2023
-
- Article
- Export citation
Kernels of localities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The affirmative answer to Singer's conjecture on the algebraic transfer of rank four
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 23 August 2022, pp. 1529-1542
- Print publication:
- October 2023
-
- Article
- Export citation
Parametrised moduli spaces of surfaces as infinite loop spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decoupling Decorations on Moduli Spaces of Manifolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 163-198
- Print publication:
- January 2023
-
- Article
- Export citation
Principal bundles on two-dimensional CW-complexes with disconnected structure group
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 675-690
- Print publication:
- September 2022
-
- Article
- Export citation
ABELIAN CYCLES IN THE HOMOLOGY OF THE TORELLI GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1703-1726
- Print publication:
- July 2023
-
- Article
- Export citation
Extensions of homomorphisms between localities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 14 September 2021, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EULER CLASSES: SIX-FUNCTORS FORMALISM, DUALITIES, INTEGRALITY AND LINEAR SUBSPACES OF COMPLETE INTERSECTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 16 July 2021, pp. 681-746
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized manifolds, normal invariants, and 𝕃-homology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 16 June 2021, pp. 574-589
-
- Article
- Export citation
Braid groups, mapping class groups and their homology with twisted coefficients
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 05 April 2021, pp. 249-266
- Print publication:
- March 2022
-
- Article
- Export citation
TAUTOLOGICAL RINGS AND STABILISATION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 17 March 2021, pp. 231-242
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Homotopic distance between maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 22 February 2021, pp. 73-93
- Print publication:
- January 2022
-
- Article
- Export citation
Homotopy of gauge groups over high-dimensional manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 05 February 2021, pp. 182-208
- Print publication:
- February 2022
-
- Article
- Export citation
Embeddings of non-simply-connected 4-manifolds in 7-space. II. On the smooth classification
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 163-181
- Print publication:
- February 2022
-
- Article
- Export citation
The Baum–Connes conjecture localised at the unit element of a discrete group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 14 January 2021, pp. 2536-2559
- Print publication:
- December 2020
-
- Article
- Export citation