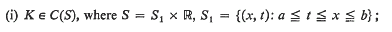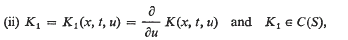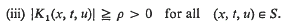Refine listing
Actions for selected content:
143 results in 41Axx
On the uniform convergence of interpolatory polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 1 / February 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 7-16
- Print publication:
- February 1979
-
- Article
-
- You have access
- Export citation
On reducing to zero the remainder of an asymptotic series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 26 / Issue 3 / November 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 309-316
- Print publication:
- November 1978
-
- Article
-
- You have access
- Export citation
An approximation property of certain nonlinear Volterra integral operators
- Part of
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 45-50
- Print publication:
- June 1976
-
- Article
- Export citation