Refine listing
Actions for selected content:
143 results in 41Axx
Positive linear operators and the approximation of continuous functions on locally compact abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 180-186
-
- Article
-
- You have access
- Export citation
Saturation on locally compact abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 255-267
-
- Article
-
- You have access
- Export citation
On the Lebesgue function for lagrange interpolation with equidistant nodes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 1 / February 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 111-118
-
- Article
-
- You have access
- Export citation
Gérard-Sibuya's versus Majima's concept of asymptotic expansion in several variables
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 21-35
-
- Article
-
- You have access
- Export citation
The Euler-Maclaurin sum formula for a closed derivation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 128-138
-
- Article
-
- You have access
- Export citation
Motion Groups and Absolutely Convergent Fourier Transforms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 3 / December 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-397
-
- Article
-
- You have access
- Export citation
Bernstein and Jackson theorems for the Heisenberg group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 241-254
-
- Article
-
- You have access
- Export citation
Operator approximations with stable elgenvalues
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 250-257
-
- Article
-
- You have access
- Export citation
Some direct and inverse theorems in approximation of functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 2 / April 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-154
-
- Article
-
- You have access
- Export citation
On the uniform convergence of interpolatory polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 1 / February 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 7-16
-
- Article
-
- You have access
- Export citation
On Hermite-Fejér interpolation with equidistant nodes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 3 / June 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 461-471
-
- Article
-
- You have access
- Export citation
Eigenelements of perturbed operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 138-148
-
- Article
-
- You have access
- Export citation
Characterization of lipschitz spaces on compact Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 200-209
-
- Article
-
- You have access
- Export citation
Direct and converse inequalities for positive linear operators on the positive semi-axis
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-103
-
- Article
-
- You have access
- Export citation
Subelliptic operators on Lie groups: regularity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 179-229
-
- Article
-
- You have access
- Export citation
On the error estimates for the Rayleigh-Schrödinger series and the Kato-Rellich perturbation series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 456-468
-
- Article
-
- You have access
- Export citation
Approximation of *-nonexpansive random multivalued operators on Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-66
-
- Article
-
- You have access
- Export citation
Best Simultaneous approximation of quasi-continuous functions by monotone functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 391-408
-
- Article
-
- You have access
- Export citation
On strongly stable approximations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 2 / April 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 251-260
-
- Article
-
- You have access
- Export citation
The degree of approximation by positive operators on compact connected abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 3 / December 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 364-373
-
- Article
-
- You have access
- Export citation
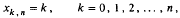
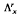 by the behavior of their best approximations by functions in the space
by the behavior of their best approximations by functions in the space 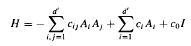
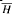 of
of