We show how one can obtain an asymptotic expression for some special functions with a very explicit error term starting from appropriate upper bounds. We will work out the details for the Bessel function $J_\nu (x)$ and the Airy function ${\rm Ai}(x).$ In particular, we answer a question raised by Olenko and find a sharp bound on the difference between $J_\nu (x)$ and its standard asymptotics. We also give a very simple and surprisingly precise approximation for the zeros ${\rm Ai}(x).$

We consider a piecewise-multilinear interpolation of a continuous random field on a d-dimensional cube. The approximation performance is measured using the integrated mean square error. Piecewise-multilinear interpolator is defined by N-field observations on a locations grid (or design). We investigate the class of locally stationary random fields whose local behavior is like a fractional Brownian field, in the mean square sense, and find the asymptotic approximation accuracy for a sequence of designs for large N. Moreover, for certain classes of continuous and continuously differentiable fields, we provide the upper bound for the approximation accuracy in the uniform mean square norm.

In this paper we deal with the operators

$$\begin{eqnarray*}{Z}_{n} (f; x)= \frac{n}{{b}_{n} } { \mathop{\sum }\nolimits}_{k= 0}^{n} {p}_{n, k} \biggl(\frac{x}{{b}_{n} } \biggr)\int \nolimits \nolimits_{0}^{\infty } {s}_{n, k} \biggl(\frac{t}{{b}_{n} } \biggr)f(t)\hspace{0.167em} dt, \quad 0\leq x\leq {b}_{n}\end{eqnarray*}$$

${p}_{n, k} (u)=\bigl(\hspace{-4pt}{\scriptsize \begin{array}{ l} \displaystyle n\\ \displaystyle k\end{array} } \hspace{-4pt}\bigr){u}^{k} \mathop{(1- u)}\nolimits ^{n- k} ,(0\leq k\leq n), u\in [0, 1] $

${s}_{n, k} (u)= {e}^{- nu} \mathop{(nu)}\nolimits ^{k} \hspace{-3pt}/ k!, u\in [0, \infty )$

We prove sufficient and necessary conditions for compactness of the Sobolev embeddings of Besov and Triebel–Lizorkin spaces defined on bounded and unbounded uniformly E-porous domains. The asymptotic behaviour of the corresponding entropy numbers is calculated. Some applications to the spectral properties of elliptic operators are described.

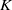Using the paths of steepest descent, we prove precise bounds with numerical implied constants for the modified Bessel function ${K}_{ir} (x)$ of imaginary order and its first two derivatives with respect to the order. We also prove precise asymptotic bounds on more general (mixed) derivatives without working out numerical implied constants. Moreover, we present an absolutely and rapidly convergent series for the computation of ${K}_{ir} (x)$ and its derivatives, as well as a formula based on Fourier interpolation for computing with many values of $r$ . Finally, we have implemented a subset of these features in a software library for fast and rigorous computation of ${K}_{ir} (x)$ .

We give a natural geometric condition that ensures that sequences of interpolation polynomials (of fixed degree) of sufficiently differentiable functions with respect to the natural lattices introduced by Chung and Yao converge to a Taylor polynomial.

The Halfin–Whitt regime, or the quality-and-efficiency-driven (QED) regime, for multiserver systems refers to a situation with many servers, a critical load, and yet favorable system performance. We apply this regime to the classical multiserver loss system with slow retrials. We derive nondegenerate limiting expressions for the main steady-state performance measures, including the retrial rate and the blocking probability. It is shown that the economies of scale associated with the QED regime persist for systems with retrials, although in situations when the load becomes extremely critical the retrials cause deteriorated performance. Most of our results are obtained by a detailed analysis of Cohen's equation that defines the retrial rate in an implicit way. The limiting expressions are established by studying prelimit behavior and exploiting the connection between Cohen's equation and Mills' ratio for the Gaussian and Poisson distributions.

The Bernstein approximation problem is to determine whether or not the space of all polynomials is dense in a given weighted ${C}_{0} $-space on the real line. A theorem of de Branges characterizes non-density by existence of an entire function of Krein class being related with the weight in a certain way. An analogous result holds true for weighted sup-norm approximation by entire functions of exponential type at most $\tau $ and bounded on the real axis ($\tau \gt 0$ fixed).

We consider approximation in weighted ${C}_{0} $-spaces by functions belonging to a prescribed subspace of entire functions which is solely assumed to be invariant under division of zeros and passing from $F(z)$ to $ \overline{F( \overline{z} )} $, and establish the precise analogue of de Branges’ theorem. For the proof we follow the lines of de Branges’ original proof, and employ some results of Pitt.

Let f ∊ C[0, 1] and let the Bn(f, q; x) be generalized Bernstein polynomials based on the q-integers that were introduced by Phillips. We prove that if f is r-monotone, then Bn(f, q; x) is r-monotone, generalizing well-known results when q = 1 and the results when r = 1 and r = 2 by Goodman et al. We also prove a sufficient condition for a continuous function to be r-monotone.

Many applications in genetic analyses utilize sampling distributions, which describe the probability of observing a sample of DNA sequences randomly drawn from a population. In the one-locus case with special models of mutation, such as the infinite-alleles model or the finite-alleles parent-independent mutation model, closed-form sampling distributions under the coalescent have been known for many decades. However, no exact formula is currently known for more general models of mutation that are of biological interest. In this paper, models with finitely-many alleles are considered, and an urn construction related to the coalescent is used to derive approximate closed-form sampling formulae for an arbitrary irreducible recurrent mutation model or for a reversible recurrent mutation model, depending on whether the number of distinct observed allele types is at most three or four, respectively. It is demonstrated empirically that the formulae derived here are highly accurate when the per-base mutation rate is low, which holds for many biological organisms.

For q>1, the set Fq of real numbers which can be expanded in base q with respect to the digit set {0,1,q} is just a self-similar set with overlaps. We consider the subset of Fq whose elements have a unique expansion and calculate its Hausdorff dimension for the case where .

We improve the degree of pointwise approximation of continuous functions f(x) by Bernstein operators, when x is close to the endpoints of [0,1]. We apply the new estimate to establish upper and lower pointwise estimates for the test function g(x)=xlog (x)+(1−x)log (1−x). At the end we prove a general statement for pointwise approximation by Bernstein operators.

We consider two problems concerning Kolmogorov widths of compacts in Banach spaces. The first problem is devoted to relations between the asymptotic behavior of the sequence of n-widths of a compact and of its projections onto a subspace of codimension one. The second problem is devoted to comparison of the sequence of n-widths of a compact in a Banach space 𝒴 and of the sequence of n-widths of the same compact in other Banach spaces containing 𝒴 as a subspace.

We consider families of general two-point quadrature formulae, using the extension of Montgomery’s identity via Taylor’s formula. The formulae obtained are used to present a number of inequalities for functions whose derivatives are from Lp spaces and Bullen-type inequalities.

We consider a nearly unstable, or near unit root, AR(1) process with regularly varying innovations. Two different approximations for the stationary distribution of such processes exist: a Gaussian approximation arising from the nearly unstable nature of the process and a heavy-tail approximation related to the tail asymptotics of the innovations. We combine these two approximations to obtain a new uniform approximation that is valid on the entire real line. As a corollary, we obtain a precise description of the regions where each of the Gaussian and heavy-tail approximations should be used.

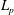
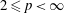
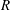
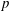
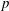
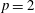
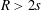
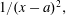
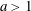
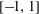
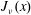
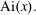
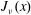
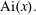
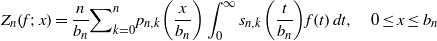
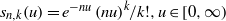
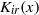
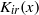
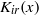
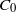
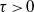
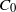
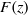
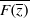
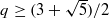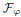In a scale of Fock spaces with radial weights ϕ we study the existence of Riesz bases of (normalized) reproducing kernels. We prove that these spaces possess such bases if and only if ϕ(x) grows at most like (log x)2.

Direct and converse theorems are established for the q-Bernstein polynomials introduced by G. M. Phillips. The direct approximation theorems are given for the second-order Ditzian–Totik modulus of smoothness. The converse results are theorems of Berens–Lorentz type.

In this paper we derive local error estimates for radial basis function interpolation on the unit sphere . More precisely, we consider radial basis function interpolation based on data on a (global or local) point set for functions in the Sobolev space with norm , where s>1. The zonal positive definite continuous kernel ϕ, which defines the radial basis function, is chosen such that its native space can be identified with . Under these assumptions we derive a local estimate for the uniform error on a spherical cap S(z;r): the radial basis function interpolant ΛXf of satisfies , where h=hX,S(z;r) is the local mesh norm of the point set X with respect to the spherical cap S(z;r). Our proof is intrinsic to the sphere, and makes use of the Videnskii inequality. A numerical test illustrates the theoretical result.

Approximations for the Stieltjes integral with (φ,Φ)-Lipschitzian integrators are given. Applications for the Riemann integral of a product and for the generalized trapezoid and Ostrowski inequalities are also provided.

In this paper we introduce a set of orthonormal functions, , where ϕn[r] is composed of a sine function and a sigmoidal transformation γr of order r>0. Based on the proposed functions ϕn[r] named by sigmoidal sine functions, we consider a series expansion of a function on the interval [−1,1] and the related convergence analysis. Furthermore, we extend the sigmoidal transformation to the whole real line ℝ and then, by reconstructing the existing sigmoidal cosine functions ψn[r] and the presented functions ϕn[r], we develop two kinds of 2-periodic series expansions on ℝ. Superiority of the presented sigmoidal-type series in approximating a function by the partial sum is demonstrated by numerical examples.