Refine listing
Actions for selected content:
143 results in 41Axx
On the Lebesgue function of weighted Lagrange interpolation. II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 145-162
-
- Article
-
- You have access
- Export citation
Tubular sets and multivariate Polya algorithm
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 232-237
-
- Article
-
- You have access
- Export citation
Inequalities and representation formulas for functions of exponential type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 15-26
-
- Article
-
- You have access
- Export citation
On reducing to zero the remainder of an asymptotic series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 26 / Issue 3 / November 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 309-316
-
- Article
-
- You have access
- Export citation
Some inequalities for trigonometric polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 216-226
-
- Article
-
- You have access
- Export citation
LOCAL RADIAL BASIS FUNCTION APPROXIMATION ON THE SPHERE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 197-224
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
APPROXIMATING THE STIELTJES INTEGRAL FOR (φ,Φ)-LIPSCHITZIAN INTEGRATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 73-90
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
SIGMOIDAL-TYPE SERIES EXPANSION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 431-450
-
- Article
-
- You have access
- Export citation
On the Asymptotic Expansion of a Class of Functions Defined by Infinite Integrals
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 183-195
- Print publication:
- December 2007
-
- Article
- Export citation
Asymptotic Expansions for Distributions of Compound Sums of Random Variables with Rapidly Varying Subexponential Distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 670-684
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Option bounds
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 145-156
- Print publication:
- 2004
-
- Article
- Export citation
Taylor's formula and preservation of generalized convexity for positive linear operators
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 765-777
- Print publication:
- September 2000
-
- Article
- Export citation
Stochastic orders in preservation properties by Bernstein-type operators
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 492-509
- Print publication:
- June 1999
-
- Article
- Export citation
Approximating integrals of stochastic processes: extensions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 843-855
- Print publication:
- December 1998
-
- Article
- Export citation
Expected measure of the union of random rectangles
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 495-500
- Print publication:
- June 1998
-
- Article
- Export citation
On the asymptotic expansion of certain functions defined by infinite series
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 401-418
- Print publication:
- December 1997
-
- Article
- Export citation
Solving the inverse problem for measures using iterated function systems: a new approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 800-820
- Print publication:
- September 1995
-
- Article
- Export citation
The mean waiting time of a GI/G/1 queue in light traffic via random thinning
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 256-266
- Print publication:
- March 1995
-
- Article
- Export citation
Approximating gamma distributions by normalized negative binomial distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 391-400
- Print publication:
- June 1994
-
- Article
- Export citation
On a new formula for the transient state probabilities for M/M/1 queues and computational implications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 237-246
- Print publication:
- March 1993
-
- Article
- Export citation
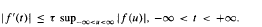 . Moreover we obtain a new representation formula for entire functions of exponential type.
. Moreover we obtain a new representation formula for entire functions of exponential type. . More precisely, we consider radial basis function interpolation based on data on a (global or local) point set
. More precisely, we consider radial basis function interpolation based on data on a (global or local) point set  for functions in the Sobolev space
for functions in the Sobolev space 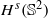 with norm
with norm 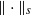 , where
, where 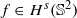 satisfies
satisfies 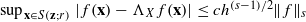 , where
, where 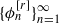 , where ϕ
, where ϕ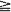 1, with invariant measures for iterated function systems by matching its moments. There are two novel features in our treatment. 1. An infinite set of fixed affine contraction maps on
1, with invariant measures for iterated function systems by matching its moments. There are two novel features in our treatment. 1. An infinite set of fixed affine contraction maps on 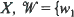 ,
, 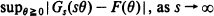 . In particular, we show that the exact order of uniform convergence is
. In particular, we show that the exact order of uniform convergence is 