We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Effective and accurate high-degree spline interpolation is still a challenging task in today’s applications. Higher degree spline interpolation is not so commonly used, because it requires the knowledge of higher order derivatives at the nodes of a function on a given mesh.
In this article, our goal is to demonstrate the continuity of the piecewise polynomials and their derivatives at the connecting points, obtained with a method initially developed by Beaudoin (1998, 2003) and Beauchemin (2003). This new method, involving the discrete Fourier transform (DFT/FFT), leads to higher degree spline interpolation for equally spaced data on an interval 
$[0,T]$. To do this, we analyze the singularities that may occur when solving the system of equations that enables the construction of splines of any degree. We also note an important difference between the odd-degree splines and even-degree splines. These results prove that Beaudoin and Beauchemin’s method leads to spline interpolation of any degree and that this new method could eventually be used to improve the accuracy of spline interpolation in traditional problems.
The Chebyshev conjecture posits that Chebyshev subsets of a real Hilbert space 
$X$ are convex. Works by Asplund, Ficken and Klee have uncovered an equivalent formulation of the Chebyshev conjecture in terms of uniquely remotal subsets of 
$X$. In this tradition, we develop another equivalent formulation in terms of Chebyshev subsets of the unit sphere of 
$X\times \mathbb{R}$. We characterise such sets in terms of the image under stereographic projection. Such sets have superior structure to Chebyshev sets and uniquely remotal sets.
Transform inversions, in which density and survival functions are computed from their associated moment generating function 
$\mathcal{M}$, have largely been based on methods which use values of 
$\mathcal{M}$ in its convergence region. Prominent among such methods are saddlepoint approximations and Fourier-series inversion methods, including the fast Fourier transform. In this paper we propose inversion methods which make use of values for 
$\mathcal{M}$ which lie outside of its convergence region and in its analytic continuation. We focus on the simplest and perhaps richest setting for applications in which 
$\mathcal{M}$ is either a meromorphic function in its analytic continuation, so that all of its singularities are poles, or else the singularities are isolated essential. Asymptotic expansions of finite- and infinite-orders are developed for density and survival functions using the poles of 
$\mathcal{M}$ in its analytic continuation. For finite-order expansions, the expansion error is a contour integral in the analytic continuation, which we approximate using the saddlepoint method based on following the path of steepest descent. Such saddlepoint error approximations accurately determine expansion errors and, thus, provide the means for determining the order of the expansion needed to achieve some preset accuracy. They also provide an additive correction term which increases accuracy of the expansion. Further accuracy is achieved by computing the expansion errors numerically using a contour path which ultimately tracks the steepest descent direction. Important applications include Wilks’ likelihood ratio test in MANOVA, compound distributions, and the Sparre Andersen and Cramér–Lundberg ruin models.
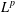$L^{p}$ -APPROXIMATION OF HOLOMORPHIC FUNCTIONS ON A CLASS OF CONVEX DOMAINS
Let 
$\unicode[STIX]{x1D6FA}$ be a member of a certain class of convex ellipsoids of finite/infinite type in 
$\mathbb{C}^{2}$ . In this paper, we prove that every holomorphic function in 
$L^{p}(\unicode[STIX]{x1D6FA})$ can be approximated by holomorphic functions on 
$\bar{\unicode[STIX]{x1D6FA}}$ in 
$L^{p}(\unicode[STIX]{x1D6FA})$ -norm, for 
$1\leq p<\infty$ . For the case 
$p=\infty$ , the continuity up to the boundary is additionally required. The proof is based on 
$L^{p}$ bounds in the additive Cousin problem.
For a prescribed set of lacunary data 
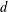
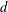
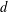
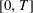
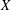
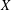
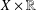
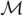
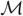
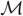
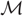
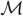
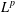
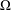
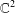
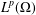
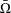
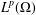
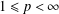
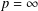
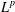
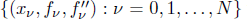with equally spaced knot sequence in the unit interval, we show the existence of a family of fractal splines 
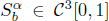satisfying 
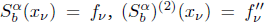for v = 0, 1, … ,N and suitable boundary conditions. To this end, the unique quintic spline introduced by A. Meir and A. Sharma [SIAM J. Numer. Anal. 10(3) 1973, pp. 433-442] is generalized by using fractal functions with variable scaling parameters. The presence of scaling parameters that add extra “degrees of freedom”, self-referentiality of the interpolant, and “fractality” of the third derivative of the interpolant are additional features in the fractal version, which may be advantageous in applications. If the lacunary data is generated from a function Φ satisfying certain smoothness condition, then for suitable choices of scaling factors, the corresponding fractal spline 
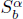satisfies 
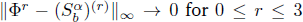, as the number of partition points increases.
Let 
$X$ be a vector space and let 
$\unicode[STIX]{x1D711}:X\rightarrow \mathbb{R}\cup \{-\infty ,+\infty \}$ be an extended real-valued function. For every function 
$f:X\rightarrow \mathbb{R}\cup \{-\infty ,+\infty \}$ , let us define the 
$\unicode[STIX]{x1D711}$ -envelope of 
$f$ by where 
$$\begin{eqnarray}f^{\unicode[STIX]{x1D711}}(x)=\sup _{y\in X}\unicode[STIX]{x1D711}(x-y)\begin{array}{@{}c@{}}-\\ \cdot \end{array}f(y),\end{eqnarray}$$
$\begin{array}{@{}c@{}}-\\ \\ \\ \cdot \end{array}$ denotes the lower subtraction in 
$\mathbb{R}\cup \{-\infty ,+\infty \}$ . The main purpose of this paper is to study in great detail the properties of the important generalized conjugation map 
$f\mapsto f^{\unicode[STIX]{x1D711}}$ . When the function 
$\unicode[STIX]{x1D711}$ is closed and convex, 
$\unicode[STIX]{x1D711}$ -envelopes can be expressed as Legendre–Fenchel conjugates. By particularizing with 
$\unicode[STIX]{x1D711}=(1/p\unicode[STIX]{x1D706})\Vert \cdot \Vert ^{p}$ , for 
$\unicode[STIX]{x1D706}>0$ and 
$p\geqslant 1$ , this allows us to derive new expressions of the Klee envelopes with index 
$\unicode[STIX]{x1D706}$ and power 
$p$ . Links between 
$\unicode[STIX]{x1D711}$ -envelopes and Legendre–Fenchel conjugates are also explored when 
$-\unicode[STIX]{x1D711}$ is closed and convex. The case of Moreau envelopes is examined as a particular case. In addition to the 
$\unicode[STIX]{x1D711}$ -envelopes of functions, a parallel notion of envelope is introduced for subsets of 
$X$ . Given subsets 
$\unicode[STIX]{x1D6EC}$ , 
$C\subset X$ , we define the 
$\unicode[STIX]{x1D6EC}$ -envelope of 
$C$ as 
$C^{\unicode[STIX]{x1D6EC}}=\bigcap _{x\in C}(x+\unicode[STIX]{x1D6EC})$ . Connections between the transform 
$C\mapsto C^{\unicode[STIX]{x1D6EC}}$ and the aforestated 
$\unicode[STIX]{x1D711}$ -conjugation are investigated.
