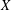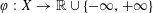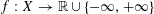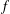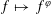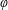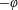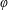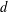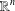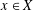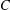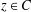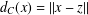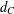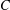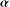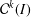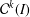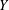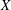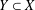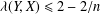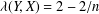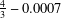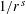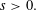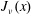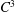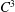Refine listing
Actions for selected content:
143 results in 41Axx
PARAMETRIC GEOMETRY OF NUMBERS IN FUNCTION FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1114-1135
- Print publication:
- 2017
-
- Article
- Export citation
ENVELOPES FOR SETS AND FUNCTIONS: REGULARIZATION AND GENERALIZED CONJUGACY
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 23 February 2017, pp. 383-432
- Print publication:
- 2017
-
- Article
- Export citation
A Multiple Interval Chebyshev-Gauss-Lobatto Collocation Method for Ordinary Differential Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 17 November 2016, pp. 619-639
- Print publication:
- November 2016
-
- Article
- Export citation
A New Quasi-Monte Carlo Technique Based on Nonnegative Least Squares and Approximate Fekete Points
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 17 November 2016, pp. 640-663
- Print publication:
- November 2016
-
- Article
- Export citation
A Fully Discrete Spectral Method for Fisher’s Equation on the Whole Line
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 19 October 2016, pp. 400-415
- Print publication:
- November 2016
-
- Article
- Export citation
On the Spurious Mode Generation Induced by Spectral-Like Optimized Interpolation Schemes Used in Computational Acoustics
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 2 / August 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 325-352
- Print publication:
- August 2016
-
- Article
- Export citation
Solution Reconstruction on Unstructured Tetrahedral Meshes Using P1-Conservative Interpolation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 847-870
- Print publication:
- October 2016
-
- Article
- Export citation
Stochastic Collocation via l1-Minimisation on Low Discrepancy Point Sets with Application to Uncertainty Quantification
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 171-191
- Print publication:
- May 2016
-
- Article
- Export citation
EXPECTATIONS OVER DETERMINISTIC FRACTAL SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 25 April 2016, pp. 171-172
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
NORMING SETS AND RELATED REMEZ-TYPE INEQUALITIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 17 November 2015, pp. 163-181
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
NEAREST POINTS AND DELTA CONVEX FUNCTIONS IN BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 September 2015, pp. 283-294
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
FRACTAL BASES FOR BANACH SPACES OF SMOOTH FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 405-419
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Staffing Many-Server Systems with Admission Control and Retrials
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 February 2016, pp. 450-475
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
HYPERPLANES OF FINITE-DIMENSIONAL NORMED SPACES WITH THE MAXIMAL RELATIVE PROJECTION CONSTANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 02 March 2015, pp. 447-463
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
FRACTAL INTERPOLATION SURFACES ON RECTANGULAR GRIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 435-446
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
CHEBYSHEV SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 161-231
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
THE BEST WEIGHTED GRADIENT APPROXIMATION TO AN OBSERVED FUNCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 54-68
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
INVERSE BERNSTEIN INEQUALITIES AND MIN–MAX–MIN PROBLEMS ON THE UNIT CIRCLE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 13 August 2014, pp. 581-590
- Print publication:
- September 2015
-
- Article
- Export citation
On the Bessel function
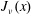 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}J_\nu (x)$ in the transition region
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}J_\nu (x)$ in the transition region
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 273-281
-
- Article
-
- You have access
- Export citation
A symmetric
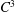 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^{3}$ non-stationary subdivision scheme
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^{3}$ non-stationary subdivision scheme
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 259-272
-
- Article
-
- You have access
- Export citation