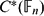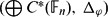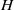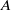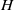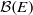Refine listing
Actions for selected content:
71 results in 16Txx
A CRITERION FOR THE JACOBSON SEMISIMPLICITY OF THE GREEN RING OF A FINITE TENSOR CATEGORY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 25 September 2017, pp. 253-272
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
BRAIDED MIXED DATUMS AND THEIR APPLICATIONS ON HOM-QUANTUM GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 231-251
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
ON GORENSTEINNESS OF HOPF MODULE ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 299-321
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
GLOBALIZATION OF TWISTED PARTIAL HOPF ACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 26 February 2016, pp. 1-28
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
THE GROUP OF BI-GALOIS OBJECTS OVER THE COORDINATE ALGEBRA OF THE FROBENIUS–LUSZTIG KERNEL OF SL(2)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 727-738
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
NON-COCOMMUTATIVE C*-BIALGEBRA DEFINED AS THE DIRECT SUM OF FREE GROUP C*-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 119-136
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
TWISTING OPERATORS, TWISTED TENSOR PRODUCTS AND SMASH PRODUCTS FOR HOM-ASSOCIATIVE ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 513-538
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
Hopfological algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 07 October 2013, pp. 1-45
- Print publication:
- January 2014
-
- Article
- Export citation
Hochschild homology of Hopf algebras and free Yetter–Drinfeld resolutions of the counit
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 17 December 2012, pp. 658-678
- Print publication:
- April 2013
-
- Article
- Export citation
The braided monoidal structures on the category of vector spaces graded by the Klein group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 613-641
-
- Article
-
- You have access
- Export citation
Module structure on Lie powers and natural coalgebra-split sub-Hopf algebras of tensor algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 04 April 2011, pp. 467-504
-
- Article
-
- You have access
- Export citation